已知命题P:“ ,都有不等式
,都有不等式 成立”,命题Q:“关于
成立”,命题Q:“关于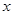 的方程
的方程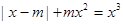 只有一个实数根”
只有一个实数根”
(Ⅰ)若命题P是真命题,求实数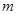 的取值集合B;
的取值集合B;
(Ⅱ)若命题“P且Q”为假,命题“P或Q”为真,求实数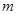 的取值范围.
的取值范围.
在四棱锥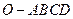 中,底面
中,底面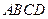 为菱形,
为菱形,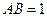 ,
,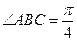 ,
,  ,
, 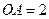 ,
,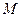 为
为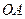 的中点,
的中点, 为
为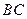 的中点
的中点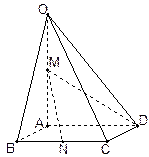
(Ⅰ)证明:直线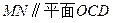
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
已知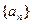 是等差数列,其前n项和为Sn,已知
是等差数列,其前n项和为Sn,已知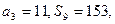
(1)求数列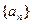 的通项公式;
的通项公式;
(2)设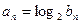 ,证明
,证明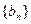 是等比数列,并求其前n项和Tn.
是等比数列,并求其前n项和Tn.
( 12分)
已知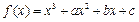 在
在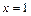 与
与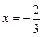 时都取得极值.
时都取得极值.
(Ⅰ)求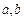 的值;
的值;
(Ⅱ)若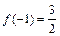 ,求
,求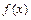 的单调区间和极值。
的单调区间和极值。
在⊿ABC中,BC=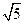 ,AC=3,sinC=2sinA
,AC=3,sinC=2sinA
(I) 求AB的值:
(II) 求sin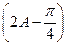 的值
的值
已知数列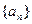 ,
,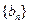 满足
满足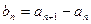 ,其中
,其中 .
.
(Ⅰ)若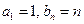 ,求数列
,求数列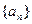 的通项公式;
的通项公式;
(Ⅱ)若 ,且
,且 .
.
(ⅰ)记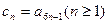 ,求证:数列
,求证:数列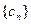 为等差数列;
为等差数列;
(ⅱ)若数列 中任意一项的值均未在该数列中重复出现无数次. 求首项
中任意一项的值均未在该数列中重复出现无数次. 求首项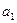 应满足的条件.
应满足的条件.