在四棱锥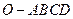 中,底面
中,底面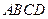 为菱形,
为菱形,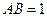 ,
,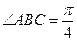 ,
,  ,
, 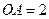 ,
,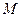 为
为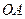 的中点,
的中点, 为
为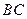 的中点
的中点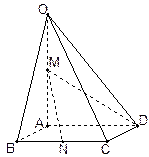
(Ⅰ)证明:直线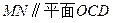
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
(理)已知动点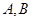 分别在
分别在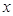 轴、
轴、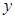 轴上,且满足
轴上,且满足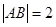 ,点
,点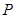 在线段
在线段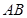 上,且
上,且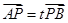
(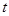 是不为零的常数)。设点
是不为零的常数)。设点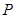 的轨迹为曲线
的轨迹为曲线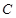 。
。
(1)求点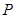 的轨迹方程;
的轨迹方程;
(2)若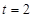 ,点
,点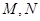 是
是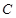 上关于原点对称的两个动点(
上关于原点对称的两个动点(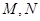 不在坐标轴上),点
不在坐标轴上),点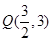 ,
,
(3)求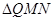 的面积
的面积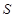 的最大值。
的最大值。
某汽车销售公司为促销采取了较灵活的付款方式,对购买10万元一辆的轿车在一年
内将款全部付清的前提下,可以选择以下两种分期付款方案购车:
方案1:分3次付清,购买后4个月第一次付款,再过4个月第二次付款,再过4个月第三次付款.
方案2:分12次付清,购买后1个月第一次付款,再过1个月第二次付款,……购买后12个月第十二次付款.现规定分期付款中,每期付款额相同,月利率为0.8%,每月利息按复利计息,试比较以上两种方案的哪一种方案付款总数较少?(参考数据:1.0083=1.024,1.0084=1.033,1.00811=1.092,1.00812=1.1)
如图,已知四棱锥P—ABCD,底面ABCD为菱形,PA 平面ABCD,
平面ABCD,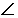 ABC=60O,E,F分别是BC,PC
ABC=60O,E,F分别是BC,PC
的中点。H为PD上的动点,EH与平面PAD所成最大角的正切值为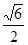 。
。
(1)证明:AE PD;
PD;
(2)求异面直线PB与AC所成的角的余弦值;
(3)若AB=2,求三棱锥P—AEF的体积。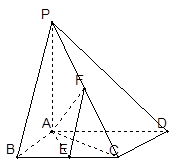
质点A位于数轴x=0处,质点B位于x=2处.这两个质点每隔1秒钟都向左或向右平移一个单位,设向左移动的概率为,向右移动的概率为.(I)求3秒后,质点A在点x=1处的概率;
(II)求2秒后,质点A、B同时在x=2处的概率.
已知 函数y=sinωx•cosωx(ω>0) (ω>0)的周期为 ,
函数y=sinωx•cosωx(ω>0) (ω>0)的周期为 ,
(I) 求ω 的值;
(II) 当0≤x≤时,求函数的最大值和最小值及相应的x的值.