(理)已知动点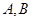 分别在
分别在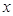 轴、
轴、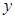 轴上,且满足
轴上,且满足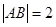 ,点
,点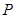 在线段
在线段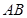 上,且
上,且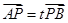
(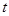 是不为零的常数)。设点
是不为零的常数)。设点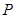 的轨迹为曲线
的轨迹为曲线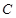 。
。
(1) 求点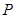 的轨迹方程;
的轨迹方程;
(2) 若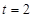 ,点
,点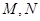 是
是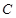 上关于原点对称的两个动点(
上关于原点对称的两个动点(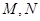 不在坐标轴上),点
不在坐标轴上),点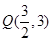 ,
,
(3) 求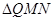 的面积
的面积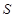 的最大值。
的最大值。
抛掷一枚质地不均匀的骰子,出现向上点数为1,2,3,4, 5, 6的概率依次记为 ,
, ,经统计发现,数列
,经统计发现,数列 恰好构成等差数列,且
恰好构成等差数列,且 是
是 的3倍.
的3倍.
(Ⅰ)求数列 的通项供式;
的通项供式;
(Ⅱ)甲、乙两人用这枚骰子玩游戏,并规定:掷一次骰子后,若向上点数为奇数,则甲获胜,否者乙获胜,请问这样的规则对甲、乙二人是否公平,请说明理由;
(Ⅲ)甲、乙丙三人用这枚骰子玩游戏,根据掷一次后向上的点数决定胜出者,并制定了公平的游戏方案,试在下面的表格中列举出两种可能的方案(不必证明)
| 方案序号 |
甲胜出对应点数 |
乙胜出对应点数 |
丙胜出对应点数 |
设△ABC的内角 的对边分别为
的对边分别为 且
且
(Ⅰ)求角A的值;
(Ⅱ)当角A钝角时,求BC边上的高.
关于 的不等式
的不等式 .
.
(Ⅰ)当 时,解此不等式;
时,解此不等式;
(Ⅱ)设函数 ,当m为何值时,
,当m为何值时, 恒成立?
恒成立?
已知在直角坐标系xOy中,直线l的参数方程为 ,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设点P是曲线C上的一个动点,求它到直线l的距离d的取值范围.
已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过点A作AD⊥CD于D,交半圆于点E,DE=1.
(Ⅰ)求证:AC平分∠BAD;
(Ⅱ)求BC的长.