(15分) 如图,金砂公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪
分成面积相等的两部分,D在AB上,E在AC上.
(Ⅰ)设AD= ,DE=
,DE= ,求
,求 关于
关于 的函数关系式;
的函数关系式;
(Ⅱ)如果DE是灌溉水管,我们希望它最短,则DE的位置应在哪里?请予以证明.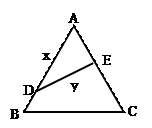
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=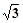 ,点F是PB的中点,点E在边BC上移动
,点F是PB的中点,点E在边BC上移动
(Ⅰ)求三棱锥E-PAD的体积;
(Ⅱ)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅲ)证明:无论点E在边BC的何处,都有PE⊥AF
已知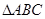 的三个顶点
的三个顶点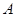 (4,0),
(4,0), (8,10),
(8,10),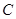 (0,6).
(0,6).
(Ⅰ)求过A点且平行于 的直线方程;
的直线方程;
(Ⅱ)求过 点且与点
点且与点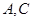 距离相等的直线方程。
距离相等的直线方程。
已知函数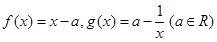 .
.
(1)判断函数 在
在 的单调性并用定义证明;
的单调性并用定义证明;
(2)令 ,求
,求 在区间
在区间 的最大值的表达式
的最大值的表达式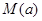 .
.
已知向量 (
( 为实数).
为实数).
(1) 时,若
时,若 ,求
,求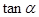 ;
;
(2)若 ,求
,求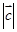 的最小值,并求出此时向量
的最小值,并求出此时向量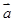 在
在 方向上的投影.
方向上的投影.
已知点 是函数
是函数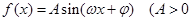 ,
, )一个周期内图象上的两点,函数
)一个周期内图象上的两点,函数 的图象与
的图象与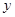 轴交于点
轴交于点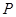 ,满足
,满足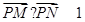 .
.
(1)求 的表达式;
的表达式;
(2)求函数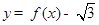 在区间
在区间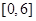 内的零点.
内的零点.