阅读下列材料，然后解答后面的问题．
我们知道方程2x+3y=12有无数组解，但在实际生活中我们往往只需要求出其正整数解．例：由2x+3y=12，得
，（x、y为正整数）∴
则有0＜x＜6．又
为正整数，则
为正整数．
由2与3互质，可知：x为3的倍数，从而x=3，代入
．
∴2x+3y=12的正整数解为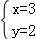
问题：
（1）请你写出方程2x+y=5的一组正整数解： ；
（2）若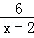
为自然数，则满足条件的x值有 个；
| A．2 | B．3 | C．4 | D．5 |
（3）七年级某班为了奖励学习进步的学生，购买了单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费35元，问有几种购买方案？
已知二次函数
的图象过点A（-3，0）和点B（1，0），且与
轴交于点C，D点在抛物线上且横坐标是 -2。
求抛物线的解析式;
抛物线的对称轴上有一动点P，求出PA+PD的最小值
点G抛物线上的动点，在x轴上是否存在点E，使B、D、E、G这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的E、G点坐标；如果不存在，请说明理由。
如图1，矩形
的顶点
为原点，点
在
上，把
沿
折叠，使点
落在
边上的点
处，点
坐标分别为
和
，抛物线
过点
.
求
两点的坐标及该抛物线的解析式；如图2，长、宽一定的矩形
的宽
，点
沿(1)中的抛物线滑动，在滑动过程中
轴，且
在
的下方，当点横坐标为-1时，点
距离
轴
个单位，当矩形在滑动过程中被轴分成上下两部分的面积比为2:3时，求点的坐标；如图3，动点
同时从点出发，点
以每秒3个单位长度的速度沿折线
按
的路线运动，点
以每秒8个单位长度的速度沿折线
按
的路线运动，当两点相遇时，它们都停止运动．设同时从点出发
秒时，
的面积为．①求出与的函数关系式，并写出的取值范围：②设
是①中函数的最大值，那么=.
如图，直线
分别交
轴、
轴于B、A两点，抛物线L：
的顶点G在轴上，且过(0，4)和(4，4)两点.
求抛物线L的解析式；
抛物线L上是否存在这样的点C，使得四边形ABGC是以BG为底边的梯形，若存在，请求出C点的坐标，若不存在，请说明理由.
将抛物线L沿
轴平行移动得抛物线L
，其顶点为P，同时将△PAB沿直线AB翻折得到△DAB，使点D落在抛物线L上. 试问这样的抛物线L是否存在，若存在，求出L对应的函数关系式，若不存在，说明理由．
已知，抛物线
与x轴交于
和
两点，与y轴交于
。
求这条抛物线的解析式和抛物线顶点M的坐标
求四边形ABMC的面积；
在对称轴的右侧的抛物线上是否存在点P，使
为直角三角形？若存在，求出所有符合条件的点P的坐标，若不存在，请说明理由
如图，已知抛物线
与
轴交于点
，与
轴交与A、B两点（点A在点B的左侧），且OA=1，OC=2
求抛物线的解析式及对称轴
点E是抛物线在第一象限内的一点，且
，求点E的坐标；在抛物线的对称轴上，是否存在点P，使得
为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由。