在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，-优题课

在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：

摸球的次数	100	200	300	500	800	1000	3000
摸到白球的次数	65	124	178	302	481	599	1803
摸到白球的频率	0.65	0.62	0.593	0.604	0.601	0.599	0.601

（1）请估计：当很大时，摸到白球的频率将会接近．（精确到0.1）
（2）假如你摸一次，你摸到白球的概率．
（3）试估算盒子里黑、白两种颜色的球各有多少只？

科目数学题型解答题难度中等

知识点：利用频率估计概率

如图1，在矩形 $ABCD$ 中， $E$ 是 $AD$ 的中点，以点 $E$ 为直角顶点的直角三角形 $EFG$ 的两边 $EF$ ， $EG$ 分别过点 $B$ ， $C$ ， $∠ F = 30 °$ ．

（1）求证： $BE = CE$ ；

（2）将 $ΔEFG$ 绕点 $E$ 按顺时针方向旋转，当旋转到 $EF$ 与 $AD$ 重合时停止转动，若 $EF$ ， $EG$ 分别与 $AB$ ， $BC$ 相交于点 $M$ ， $N$ （如图 $2)$ ．

①求证： $ΔBEM ≅ ΔCEN$ ；

②若 $AB = 2$ ，求 $ΔBMN$ 面积的最大值；

③当旋转停止时，点 $B$ 恰好在 $FG$ 上（如图 $3)$ ，求 $\sin ∠ EBG$ 的值．

益马高速通车后，将桃江马迹塘的农产品运往益阳的运输成本大大降低，马迹塘一农户需要将 $A$ ， $B$ 两种农产品定期运往益阳某加工厂，每次运输 $A$ ， $B$ 产品的件数不变，原来每运一次的运费是1200元，现在每运一次的运费比原来减少了300元． $A$ ， $B$ 两种产品原来的运费和现在的运费（单位：元 $/$ 件）如下表所示：

品种	$A$	$B$
原运费	45	25
现运费	30	20

（1）求每次运输的农产品中 $A$ ， $B$ 产品各有多少件？

（2）由于该农户诚实守信，产品质量好，加工厂决定提高该农户的供货量，每次运送的产品总件数增加8件，但总件数中 $B$ 产品的件数不得超过 $A$ 产品件数的2倍，问产品件数增加后，每次运费最少需要多少元？

如图，在平面直角坐标系中有三点 $(1, 2)$ ， $(3, 1)$ ， $(- 2, - 1)$ ，其中有两点同时在反比例函数 $y = \frac{k}{x}$ 的图象上，将这两点分别记为 $A$ ， $B$ ，另一点记为 $C$ ．

（1）求出 $k$ 的值；

（2）求直线 $AB$ 对应的一次函数的表达式；

（3）设点 $C$ 关于直线 $AB$ 的对称点为 $D$ ， $P$ 是 $x$ 轴上的一个动点，直接写出 $PC + PD$ 的最小值（不必说明理由）．

2018年湖南省进入高中学习的学生三年后将面对新高考，高考方案与高校招生政策都将有重大变化．某部门为了了解政策的宣传情况，对某初级中学学生进行了随机抽样调查，根据学生对政策的了解程度由高到低分为 $A$ ， $B$ ， $C$ ， $D$ 四个等级，并对调查结果分析后绘制了如下两幅不完整的统计图，请你根据图中提供的信息完成下列问题：

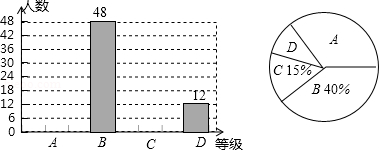
（1）求被调查学生的人数，并将条形统计图补充完整；

（2）求扇形统计图中的 $A$ 等对应的扇形圆心角的度数；

（3）已知该校有1500名学生，估计该校学生对政策内容了解程度达到 $A$ 等的学生有多少人？

如图， $AB / / CD$ ， $∠ 1 = ∠ 2$ ．求证： $AM / / CN$ ．