如图,在平面直角坐标系中,点A、B分别在x轴y轴的正半轴上,线段OA的长是不等式5x﹣4<3(x+2)的最大整数解,线段OB的长是一元二次方程x2﹣2x﹣3=0的一个根,将Rt△ABO沿BE折叠,使AB边落在OB边所在的y轴上,点A与点D重合.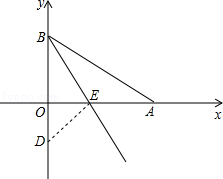
(1)求OA、OB的长;
(2)求直线BE的解析式;
(3)在平面内是否存在点M,使B、O、E、M为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
已知x、y为实数,y= 求3x+4y
求3x+4y
先化简,再求值: ,其中a=
,其中a= +1.
+1.
如图所示,一个点从数轴上的原点开始,先向右移动3单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照下列图象并思考,完成下列各题:
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_______,A,B两点间的距离是________;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是_______,A,B两点间的距离为________;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_________,A,B两点间的距离是________.
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么,请你求出终点B表示什么数?A,B两点间的距离为多少?
在修我县人民路的BRT(快速公交)时,需要对部分建筑进行拆迁,县政府成立了拆迁工作组,他们步行去做拆迁产生的思想工作;如果向南记为负,向北记为正;以下是他们一天中行程(单位:km):出发点,-0.7,+2.7,-1.3,+0.3,-1.4,+2.6,拆迁点;
(1)工作组最后到达的地方在出发点的哪个方向?距出发点多远?
(2)在一天的工作中,最远处距离出发点有多远?
(3)如果平均每个拆迁地址(出发点处没有拆迁)要做1小时的思想工作,他的步行速度为2km/h,工作组早上九点出发,做完工作时是下午几点?
“囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为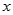 、
、 ,剪去的两个小直角三角形的两直角边长也分别为
,剪去的两个小直角三角形的两直角边长也分别为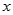 、
、 .
.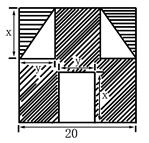
(1)用含有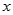 、
、 的代数式表示下图中“囧”的面积;
的代数式表示下图中“囧”的面积;
(2)当 =6,
=6,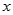 =8时,求此时“囧”的面积.
=8时,求此时“囧”的面积.