某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数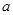 .
.
①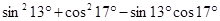 ;
;
② ;
;
③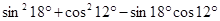 ;
;
④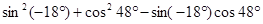 ;
;
⑤ .
.
(1)从上述五个式子中选择一个,求出常数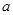 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
(本小题满分15分)将进货单价为80元的商品按90元一个售出时,能卖出400个,已知这种商品每个涨价1元,其销售量就减少10个,为了取得最大利润,每个售价应定为多少元?
(本小题满分13分)已知函数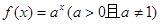 经过点
经过点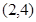 .
.
(1)求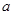 的值;(2)求
的值;(2)求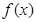 在[0,1]上的最大值与最小值.
在[0,1]上的最大值与最小值.
(本小题满分14分)如图椭圆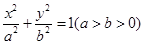 的上顶点为A,左顶点为B, F为右焦点, 过F作平行于AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。
的上顶点为A,左顶点为B, F为右焦点, 过F作平行于AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。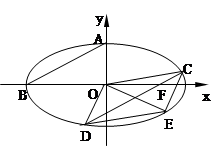
(Ⅰ)求椭圆的离心率;
(Ⅱ)若平行四边形OCED的面积为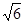 , 求椭圆的方程.
, 求椭圆的方程.
(本小题满分14分)过点(1,0)直线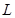 交抛物线
交抛物线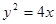 于A(x1,y1),B(x2,y2)两点,抛物线的顶点是
于A(x1,y1),B(x2,y2)两点,抛物线的顶点是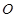 .
.
(ⅰ)证明: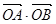 为定值;
为定值;
(ⅱ)若AB中点横坐标为2,求AB的长度及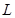 的方程.
的方程.
(本小题满分14分)如图,长方体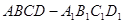 中,
中,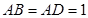 ,
,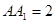 ,
, 为
为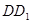 的中点。
的中点。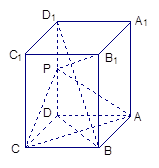
(1)求证:直线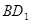 ∥平面
∥平面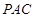 ;
;
(2)求证:平面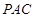
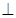 平面
平面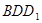 ;
;
(3)求证:直线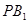
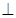 平面
平面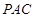 。
。