已知函数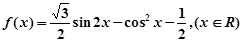
(1)当 时,求函数
时,求函数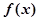 的最小值和最大值;
的最小值和最大值;
(2)设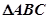 的内角
的内角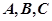 的对应边分别为
的对应边分别为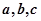 ,且
,且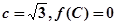 ,若向量
,若向量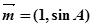 与向量
与向量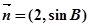 共线,求
共线,求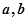 的值.
的值.
(本小题满分10分)设动点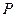 到点
到点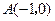 和
和 的距离分别为
的距离分别为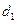 和
和 ,
,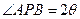 ,且存在常数
,且存在常数 ,使得
,使得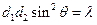
(1)证明:动点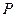 的轨迹
的轨迹 为双曲线,并求出
为双曲线,并求出 的方程;
的方程;
(2)过点 作直线交双曲线
作直线交双曲线 的右支于
的右支于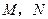 两点,试确定
两点,试确定 的范围,使
的范围,使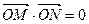 ,其中点
,其中点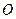 为坐标原点
为坐标原点 
(本小题满分10分) 已知 ;
; 若
若 是
是 的必要非充分条件,求实数
的必要非充分条件,求实数 的取值范围
的取值范围
(本小题满分8分)2007年9月5日生效的一年期个人贷款利率为7.29%,小陈准备购买一部汽车,购车一年后一次性付清车款,这时正好某商业银行推出一种一年期优惠贷款业务,年利率为 ,且
,且
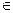 (0.045,0.062),贷款量与利率的平方成正比,因此,小陈申请这种一年期优惠贷款.
(0.045,0.062),贷款量与利率的平方成正比,因此,小陈申请这种一年期优惠贷款.
(1)写出小陈应支付的利息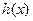 ;
;
(2) 一年期优惠利率 为多少时,利息差最大?
为多少时,利息差最大?
(本小题满分8分)已知顶点在原点,焦点在 轴上的抛物线与直线
轴上的抛物线与直线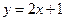 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|=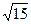 ,求抛物线的方程
,求抛物线的方程
(本小题满分8分) 设
(1)求函数f(x)的单调区间.(2)求极值点与极值.