如图,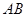 为圆
为圆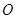 的直径,点
的直径,点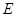 、
、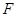 在圆
在圆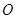 上,矩形
上,矩形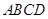 所在的平面和圆
所在的平面和圆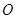 所在的平面互相垂直,且
所在的平面互相垂直,且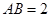 ,
, .
.
(Ⅰ)求证: 平面
平面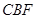 ;
;
(Ⅱ)求三棱锥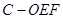 的体积.
的体积.
(本小题满分12分)某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一
人答一份).现从回收的年龄在20~60岁的问卷中随机抽取了100份,统计结果如下面的图表所示.
| 年龄 分组 |
抽取份数 |
答对全卷 的人数 |
答对全卷的人数 占本组的概率 |
| [20,30) |
40 |
28 |
0.7 |
| [30,40) |
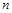 |
27 |
0.9 |
| [40,50) |
10 |
4 |
 |
| [50,60] |
20 |
 |
0.1 |

(1)分别求出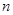 ,
,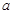 ,
, ,
,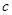 的值;
的值;
(2)从年龄在 答对全卷的人中随机抽取2人授予“环保之星”,求年龄在
答对全卷的人中随机抽取2人授予“环保之星”,求年龄在 的人中至少有1
的人中至少有1
人被授予“环保之星”的概率.
(本小题满分12分)已知△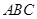 的三边
的三边 ,
,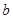 ,
, 所对的角分别为
所对的角分别为 ,
,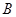 ,
, ,且
,且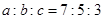 .
.
(1)求 的值;
的值;
(2)若△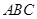 外接圆的半径为14,求△
外接圆的半径为14,求△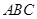 的面积.
的面积.
(本小题满分14分)已知函数
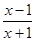 ,
,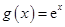 (其中
(其中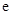 为自然对数的底数).
为自然对数的底数).
(1)若函数 在区间
在区间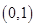 内是增函数,求实数
内是增函数,求实数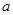 的取值范围;
的取值范围;
(2)当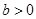 时,函数
时,函数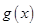 的图象
的图象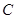 上有两点
上有两点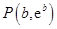 ,
,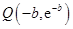 ,过点
,过点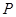 ,
,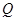 作图象
作图象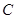 的切线分
的切线分
别记为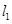 ,
,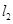 ,设
,设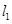 与
与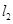 的交点为
的交点为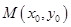 ,证明
,证明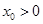 .
.
(本小题满分14分)已知圆心在 轴上的圆
轴上的圆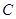 过点
过点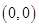 和
和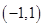 ,圆
,圆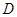 的方程为
的方程为 .
.
(1)求圆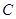 的方程;
的方程;
(2)由圆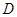 上的动点
上的动点 向圆
向圆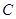 作两条切线分别交
作两条切线分别交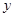 轴于
轴于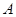 ,
,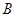 两点,求
两点,求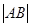 的取值范围.
的取值范围.
(本小题满分14分)已知点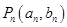
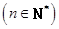 在直线
在直线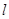 :
: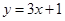 上,
上,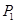 是直线
是直线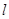 与
与 轴的
轴的
交点,数列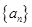 是公差为1的等差数列.
是公差为1的等差数列.
(1)求数列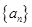 ,
,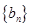 的通项公式;
的通项公式;
(2)求证: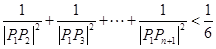 .
.