已知函数f(x)=log2(x+m),且f(0)、f(2)、f(6)成等差数列.
(1)求实数m的值;
(2)若a、b、c是两两不相等的正数,且a、b、c成等比数列,试判断f(a)+f(c)与2f(b)的大小关系,并证明你的结论.
如图,△ABC中, .求AC的长.
.求AC的长.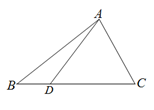
设一元二次不等式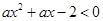 的解集为
的解集为 .
.
(Ⅰ)当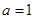 时,求
时,求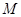 ;
;
(Ⅱ)当 时,求
时,求 的取值范围.
的取值范围.
(本小题满分12分)
某小型餐馆一天中要购买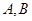 两种蔬菜,
两种蔬菜,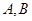 蔬菜每公斤的单价分别为2元和3 元.根据需要,
蔬菜每公斤的单价分别为2元和3 元.根据需要,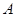 蔬菜至少要买6公斤,
蔬菜至少要买6公斤,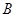 蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,
蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,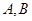 两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
(本小题满分10分)
在 中,角
中,角 所对的边分别为
所对的边分别为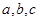 .已知
.已知 ,
, ,
,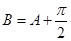 .
.
(Ⅰ)求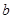 的值;
的值;
(Ⅱ)求 的面积.
的面积.
(本小题满分10分)
等差数列 的前n项和为
的前n项和为 ,已知
,已知 ,
, .
.
(Ⅰ)求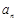 及
及 ;
;
(Ⅱ)令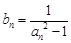 (
( ),求数列
),求数列 的前n项和
的前n项和 .
.