某车间将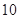 名技工平均分为甲、乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
名技工平均分为甲、乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
| |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲组 |
4 |
5 |
7 |
9 |
10 |
| 乙组 |
5 |
6 |
7 |
8 |
9 |
(1)分别求出甲、乙两组技工在单位时间内完成合格零件的平均数及方差,并由此比较两组技工的技术水平;
(2)质检部门从该车间甲、乙两组中各随机抽取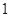 名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过
名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过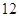 件,则称该车间“质量合格”,求该车间“质量合格”的概率.
件,则称该车间“质量合格”,求该车间“质量合格”的概率.
(本小题满分14分)
已知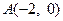 ,
,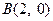 为椭圆
为椭圆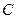 的左、右顶点,
的左、右顶点, 为其右焦点,
为其右焦点,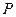 是椭圆
是椭圆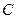 上异于
上异于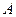 ,
, 的动点,且
的动点,且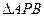 面积的最大值为
面积的最大值为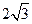 .
.
(Ⅰ)求椭圆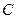 的方程及离心率;
的方程及离心率;
(Ⅱ)直线 与椭圆在点
与椭圆在点 处的切线交于点
处的切线交于点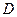 ,当直线
,当直线 绕点
绕点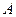 转动时,试判断以
转动时,试判断以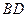

为直径的圆与直线 的位置关系,并加以证明.
的位置关系,并加以证明.
(本小题满分13分)
已知函数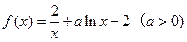 .
.
(Ⅰ)若曲线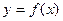 在点
在点 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数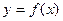 的单调区间;
的单调区间;
(Ⅱ)若对于 都有
都有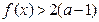 成立,试求
成立,试求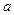 的取值范围;
的取值范围;
(Ⅲ)记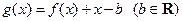 .当
.当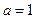 时,函数
时,函数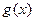 在区间
在区间 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围.
(本小题满分13分)
在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖. 已知教师甲投进每个球的概率都是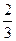 .
.
( Ⅰ)记教师甲在每场
Ⅰ)记教师甲在每场 的6次投球中投进球的个数为X,求X的分布列及数学期望;
的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率;
(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比 赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
(本小题满分13分)
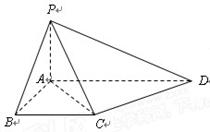
如图,在四棱锥 中,底面
中,底面 为直角
为直角 梯形,且
梯形,且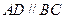 ,
,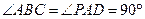 ,侧面
,侧面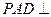 底面
底面 . 若
. 若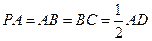 .
.
(Ⅰ)求证: 平面
平面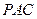 ;
;
(Ⅱ)侧棱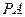 上是否存在点
上是否存在点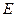 ,使得
,使得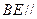 平面
平面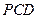 ?若存在,指出点
?若存在,指出点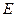 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(本小题满分13分)
在锐角 中,角
中,角 ,
,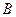 ,
, 所对的边分别为
所对的边分别为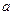 ,
, ,
, .已知
.已知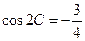 .
.
(Ⅰ)求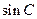 ;
;
(Ⅱ)当 ,且
,且 时,求
时,求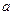 .
.