已知数列 的前
的前 项和为
项和为 ,且有
,且有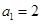 ,
,
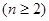 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(Ⅲ)若 ,且数列
,且数列 中的 每一项总小于它后面的项,求实数
中的 每一项总小于它后面的项,求实数 的取值范围.
的取值范围.
各项均为正数的数列 的前
的前 项和为
项和为 ,满足
,满足
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,
,
数列 满足
满足 ,数列
,数列 的前
的前
 项和为
项和为 ,求
,求 ;
;
(3)若数列 ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的 ,试图确定
,试图确定 的值是否可以等于2011?为此,他设计了一个程序
的值是否可以等于2011?为此,他设计了一个程序 (如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
已知关于 的不等式
的不等式 ,其中
,其中
 。
。
(1)求上述不等式的解;
(2)是否存在实数 ,使得上述不等式的解集
,使得上述不等式的解集 中只有有限个整数?若存在
中只有有限个整数?若存在 ,求出使得
,求出使得 中整数个数最少的
中整数个数最少的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
设函数 。
。
(1)当 时,求函数
时,求函数 的最小值;
的最小值;
(2)当 时,试判断函数
时,试判断函数 的单调性,并证明。
的单调性,并证明。
在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 。
。
(1)求 的值;
的值;
(2)若 ,且
,且 ,求
,求 和
和 的值
的值
设二次函数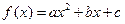 在区间
在区间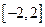 上的最大值、最小值分别是M、m,集合
上的最大值、最小值分别是M、m,集合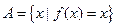 .
.
(1)若 ,且
,且 ,求M和m的值;
,求M和m的值;
(2)若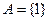 ,且
,且 ,记
,记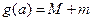 ,求
,求 的最小值.
的最小值.