某数学兴趣小组在上课时,老师为他们设计了一个抓奖游戏,并设置了两种抓奖方案,游戏规则是:在一个不透明的箱子内放了3颗表面写有-2,-1,1且大小完全相同的小球,每个游戏者必须抓两次小球;分别以先后抓到的两个小球所标的数字作为一个点的横、纵坐标,如果这个点在第三象限则中奖.有两种方案如下:
方案一:先抓出一颗小球,放回去摇匀后再抓出一颗小球;
方法二:先抓出一颗小球且不放回,然后再抓出一颗小球;
(1)请你计算(列表或画树形图)方案一的中奖率;
(2)请直接写出方案二的中奖概率,如果你在做这个游戏,你会选择方案几?说明理由.
甲、乙、丙三个工程队单独完成某项工程,分别需要140小时、87.5小时、77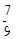 时。现在,甲和乙都最多只能工作60小时,丙最多只能工作35小时,三队工作时间之和为100小时完成工程,则甲最多工作多少小时?
时。现在,甲和乙都最多只能工作60小时,丙最多只能工作35小时,三队工作时间之和为100小时完成工程,则甲最多工作多少小时?
如果一个自然数n能被不超过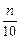 的所有的非0自然数整除,我们称自然数n为“牛数”。
的所有的非0自然数整除,我们称自然数n为“牛数”。
请写出所有的牛数。
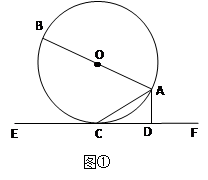
如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D。求证:∠DAC=∠BAC;
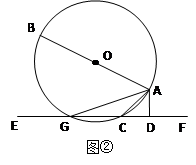
若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论。
把一副三角板如图甲放置,其中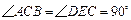 ,
, ,
, ,斜边
,斜边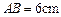 ,
,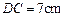 。把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙)。这时AB与CD1相交于点
。把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙)。这时AB与CD1相交于点 ,与D1E1相交于点F。
,与D1E1相交于点F。求
 的度数;
的度数;求线段AD1的长;
若把三角形D1CE1绕着点
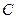 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由。
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由。

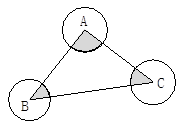
如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少?