某校为了满足学生借阅图书的需求，计划购买一批新书，为此可，该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计，结果如下图.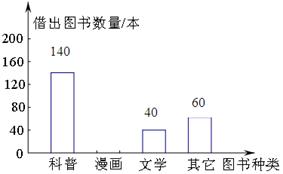
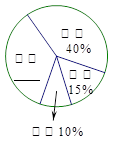
请你根据统计图中的信息，解答下列问题：
（1）补全条形统计图和扇形统计图；
（2）该校学生最喜欢借阅哪类图书？
（3）该校计划购买新书600本，若按扇形统计图中的百分比来相应地确定漫画、科普、文学、其他这四类图书的购买量，求应购买这四类图书各多少本？
计算：
.
如图，直线y=hx+d与x轴和y轴分别相交于点A(-1,0),B(0,1),与双曲线y=
在第一象限相交于点C；以AC为斜边、
为内角的直角三角形，与以CO为对角线、一边在x轴上的矩形面积相等；点C,P在以B为顶点的抛物线y=
上；直线y=hx+d、双曲线y=和抛物线
同时经过两个不同的点C，D
（1）确定t的值
（2）确定m , n , k的值
（3）若无论a , b , c何值，抛物线都不经点P，请确定P坐标
如图①，P是△ABC边AC上的动点，以P为顶点作矩形PDEF，顶点D,E在边BC上，顶点F在边AB上；△ABC的底边BC及BC上的高的长分别为a , h,且是关于x的一元二次方程
的两个实数根，设过D, E,F三点的⊙O的面积为
,矩形PDEF的面积为
（1）求证：以a+h为边长的正方形面积与以a、h为边长的矩形面积之比不小于4；
（2）求
的最小值；
（3）当的值最小时，过点A作BC的平行线交直线BP与Q，这时线段AQ的长与m , n , k的取值是否有关？请说明理由。
【函函游园记】
函函早晨到达上海世博园D区入口处等待开园，九时整开园，D区入口处有10n条安全检查通道让游客通过安检入园，游客每分钟按相同的人数源源不断到达这里等待入园，直到中午十二时D区入口处才没有排队人群，游客一到就可安检入园。九时二十分函函通过安检进入上海世博园时，发现平均一个人通过安全检查通道入园耗时20秒。
【排队的思考】
（1）若函函在九时整排在第3000位，则这时D区入口安检通道可能有多少条？
（2）若九时开园时等待D区入口处的人数不变：当安检通道是现有的1.2倍且每分钟到达D区入口处的游客人数不变时，从中午十一时开始游客一到D区入口处就可安检入园；当每分钟到达D区入口处的游客人数增加了50%，仍要求从十二时开始游客一到D区入口处就可安检入园，求这时需要增加安检通道的数量。
已知Rt△ABC和Rt△EBC，
°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切，D为切点，AD//BC。
（1）用尺规确定并标出圆心O；（不写做法和证明，保留作图痕迹）
（2）求证：
（3）若AD=1，
，求BC的长。