以下是根据某电脑专卖店销售的相关数据绘制的统计图的一部分．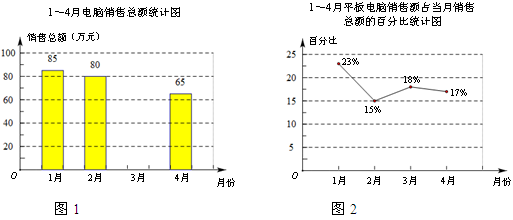
请根据图1、图2解答下列问题：
（1）来自该店财务部的数据报告表明，1～4月的电脑销售总额一共是290万元，请将图1中的统计图补充完整；
（2）该店1月份平板电脑的销售额约为 万元（结果精确到0．1）；
（3）小明观察图2后认为，4月份平板电脑的销售额比3月份减少了，你同意他的看法吗？请说明理由．
如图，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．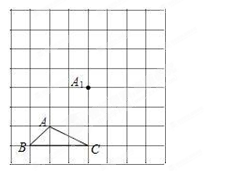
（1）把△ABC沿BA方向平移后，点A移到点A1，在网格中画出平移后得到的△A1B1C1；
（2）把△A1B1C1绕点A1按逆时针方向旋转90°，在网格中画出旋转后的△A1B2C2；
（3）如果网格中小正方形的边长为1，求点B经过（1）、（2）变换的路径总长．
已知圆锥的底面直径是8，母线长是16，求它的侧面展开图的圆心角与圆锥的全面积。
如图，已知二次函数图象顶点为C（1，0），直线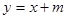
与该二次函数交于A，B两点，其中A点（3，4），B点在y轴上，
（1）求m值及这个二次函数关系式；
（2）P为线段AB上一动点（P不与A，B重合），过P做x轴垂线与二次函数交于点E，设线段PE长为h，点P横坐标为x，求h与x之间的函数关系式，并写出自变量x取值范围；
（3）D为AB线段与二次函数对称轴的的交点，在AB上是否存在一点P，使四边形DCEP为平行四边形？若存在，请求出P点坐标；若不存在，请说明理由。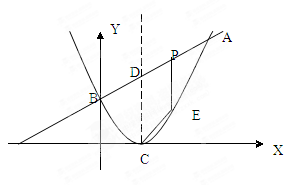
2011年国家对“酒后驾车”加大了处罚力度，出台了不准酒后驾车的禁令，某记者在一停车场对开车的司机进行了相关的调查，本次调查结果共有四种情况：①有时会喝点酒开车；②已戒酒或从不喝酒；③酒后不开车或请专业司机代驾；④平时喝酒，但开车当天不喝酒。将这次调查情况整理并绘制成如下尚不完整的统计图，请根据相关信息，解答下列问题。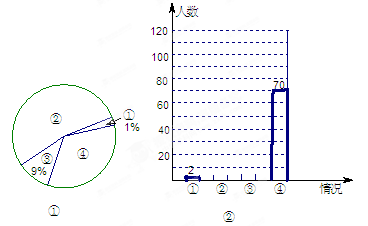
（1）该记者本次一共调查
了名司机。
（2）求图①中④所在扇形的圆心角，并补全图②。
（3）在本次调查中，记者随机采访其中一名司机，求他属于第②种情况的概率。
（4）请估计在开车的10万名司机中，不违反“酒驾”禁令的人数。
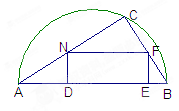
如图，在直径为AB的一块半圆形土地上，画出一块三角形区域，使三角形的一边为AB，顶点C在半圆上，其它两边长分别为6cm和8cm，现要建造一个内接于△ABC的矩形水池DEFN，其中DE在AB上，如图所示的设计方案是使AC=8cm，BC=6cm。
（1）求△ABC中AB边上的高h；
（2）设DN=x，当x取何值时，水池DEFN的面积最大？
（3）实际施工时，发现在AB上距B点1.85m处有一棵大树，则这棵大树是否位于最大矩形的边上？如果在，为了保护大树，请你设计出另外的方案，使内接于满足条件的三角形中建最大矩形水池能避开大树。