已知A、B两地的路程为240
 .某经销商每天都要用汽车或火车将
.某经销商每天都要用汽车或火车将
 保鲜品一次性由A地运往B地.受各种因素限制,下周只能采取用汽车和火车中的一种进行运输且需提前预定.现有货运收费项目及收费标准表、行驶路
保鲜品一次性由A地运往B地.受各种因素限制,下周只能采取用汽车和火车中的一种进行运输且需提前预定.现有货运收费项目及收费标准表、行驶路 /
/
 与行驶时间
与行驶时间 /s的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
/s的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
| 运输工具 |
运输费单价元/( · ·  ) ) |
冷藏费单价元/( ·h) ·h) |
固定费用元/次 |
| 汽车 |
2 |
5 |
200 |
| 火车 |
1.6 |
5 |
2280 |
(1)汽车的速度为 
 /h,火车的速度为
/h,火车的速度为 
 /h;
/h;
(2)设每天用汽车和火车运输的总费用分别为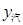 /元和
/元和 /元,分别求
/元,分别求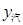 、
、 与
与 的函数关系式(不必写出
的函数关系式(不必写出 的取值范围),及
的取值范围),及 为何值时
为何值时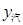 >
> ;
;
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输费用较省?
如图,已知△ABC是等腰三角形,顶角∠BAC=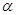 (
(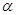 <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转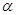 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF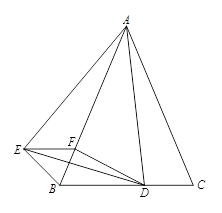
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
某公司拟用运营指数y来量化考核司机的工作业绩,运营指数(y)与运输次数(n)和平均速度(x)之间满足关系式为y=ax2+bnx+100,当n=1,x=30时,y=190;当n=2,x=40时,y=420
用含x和n的式子表示y;
当运输次数定为3次,求获得最大运营指数时的平均速度;
若n=2,x=40,能否在n增加m%(m>0),同时x减少m%的情况下,而y的值保持不变,若能,求出m的值;若不能,请说明理由。
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(- ,
, )
)
在一块长16m、宽12m的矩形荒地上,小明要建造一个花园,并使花园所占的面积为荒地面积的一半,其中花园四周小路的宽度都相等,求小路的宽。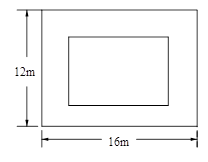
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,-1),B(-5 ,-4),C(-2 ,-3)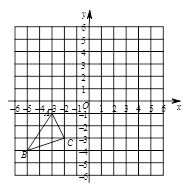
(1)作出△ABC向上平移6个单位,再向右平移7个单位的△A1B1C1
(2)作出△ABC关于y轴对称的△A2B2C2,并写出点C2的坐标;
(3)将△ABC绕点O顺时针旋转900后得到△A3B3C3,请你画出旋转后的△A3B3C3
如果关于x的一元二次方程x2+4x+a=0的两个不相等的实数根x1,x2满足x1x2-2xx-2x2-5=0,求a的值