如图,在棱长为1的正方体 中.
中.
⑴求异面直线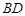 与
与 所成的角;
所成的角;
⑵求证:平面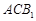
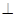 平面
平面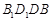 .
.
如图,正三棱柱ABC—A1B1C1的底面边长为a,点M在边 BC上,△AMC1是以点M为直角顶点的等腰直角三角形。
(Ⅰ)求证点M为边BC的中点;
(Ⅱ)求点C到平面AMC1的距离;
(Ⅲ)求二面角M—AC1—C的大小。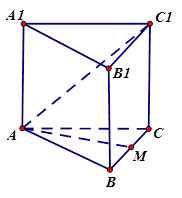
已知函数
(I)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(II)设△ 的内角
的内角 对边分别为
对边分别为 ,且
,且 ,若
,若 与
与 共线,求
共线,求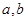 的值.
的值.
已知函数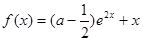 .(
.( )
)
(1)若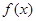 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)若在区间 上,函数
上,函数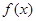 的图象恒在曲线
的图象恒在曲线 下方,求
下方,求 的取值范围.
的取值范围.
已知递增等差数列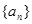 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列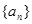 的通项公式
的通项公式 ;
;
(2)若不等式 对任意
对任意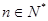 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
已知函数 .
.
(1)求 在区间
在区间 上的最大值;
上的最大值;
(2)若函数 在区间
在区间 上存在递减区间,求实数m的取值范围.
上存在递减区间,求实数m的取值范围.