如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)图②中的阴影部分的正方形的边长等于_________(用含m、n的代数式表示);
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①_____________________.方法②____________________;
(3)观察图②,试写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系
__________________________________________________________________
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,求(a-b)2的值.
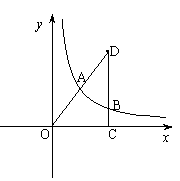
已知:如图,在直角坐标系xOy中,Rt△OCD的一边OC在x轴上.∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.求该反比例函数的解析式;
若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求经过O、A、B三点的抛物线的解析式.
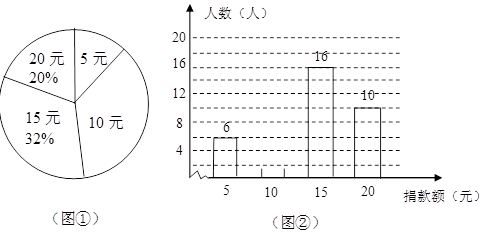
为支援“玉树抗震救灾”,在一次爱心捐款活动中,九(1)班同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有5元、10元、15元、20元共四种情况.根据统计数据绘制了图①和图②两幅尚不完整的统计图.该班共有_____________名同学,学生捐款的众数是______________;
请你将图②的统计图补充完整;
计算该班同学平均捐款多少元?
从这个班任意抽取一名学生,这名学生捐款额为10元以上(不含10元)的概率是多少?
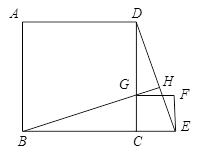
如图, 是同一直线上的三个点,四边形
是同一直线上的三个点,四边形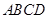 与四边形
与四边形 都是正方形,连结
都是正方形,连结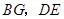 .
.观察图形,猜想
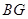 与
与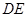 之间的大小关系,并证明你的结论;
之间的大小关系,并证明你的结论;若延长
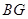 交
交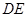 于点
于点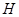 ,求证:
,求证: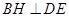 .
.
三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.
在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);
△BCD是不是黄金三角形,如果是,请给出证明;如果不是,请说明理由;
设
 ,试求k的值;
,试求k的值;如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,
请直接写出 的值.
的值.
已知二次函数的图象与x轴只有一个交点A(-2,0)、与y轴的交点为B(0,4),且其对称轴与y轴平行.求该二次函数的解析式,并在所给坐标系中画出它的大致图象;
在二次函数位于A、B两点之间的图象上取一点M,过点M分别作x轴、y轴的垂线,垂足分别为点C、D.求矩形MCOD的周长的最小值和此时的点M的坐标.
