设命题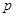
：关于
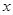的方程
无实根；命题
：函数
的定义域为
，若命题"p或q”是真命题，“p且q”是假命题，求实数a的取值范围．
若过定点A（2，0）的直线交椭圆
+y2=1于不同的两点E、F（点E在点A、F之间），且满足
=m
，求实数m的取值范围．
设
＝（4，-3），
＝（2，1），是否存在实数t，使得+t与的夹角为45º．若存在，求出t的值，若不存在说明理由．
已知
，
，
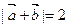．是否存在实数
，使得
．若存在，求出的值，若不存在，说明理由．
已知O为坐标原点，点A、B的坐标分别为A（a，0）、B（0，a），其中常数a>0，点P在线段AB上，且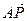
=λ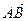
（0≤λ≤1），求
·
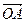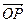的最大值．
若f（x）=2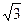
sin
cos－2sin2．（1）若x∈[0，π]，求f（x）的值域；（2）在△ABC中，A、B、C所对边分别为a、b、c，若f（C）=1，且b2=ac，求sinA的值．