设 是定义在
是定义在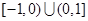 上的函数,当
上的函数,当 ,且
,且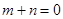 时,有
时,有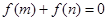 .
.
(1)证明 是奇函数;
是奇函数;
(2)当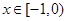 时,
时, (a为实数). 则当
(a为实数). 则当 时,求
时,求 的解析式;
的解析式;
(3)在(2)的条件下,当 时,试判断
时,试判断 在
在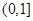 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
(本小题满分12分)为应对金融危机,刺激消费,某市给市民发放面额为100元 的旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
的旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
  |
200元 |
300元 |
400元 |
500元 |
| 老年 |
0.4 |
0.3 |
0.2 |
0.1 |
| 中年 |
0.3 |
0.4 |
0.2 |
0.1 |
| 青年 |
0.3 |
0.3 |
0.2 |
0.2 |
某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点,(1)求这三人恰有两人消费额不少于300元的概率;(2)求这三人消费总额大于或等于1300元的概率。
(本小题满分12分)函数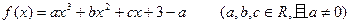 当
当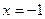 时,
时,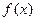 取得极大值2(1)用关于
取得极大值2(1)用关于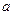 的代数式分别表示
的代数式分别表示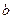 与
与 。(2)求
。(2)求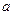 的取值范围。
的取值范围。
(本小题满分12分)已知向量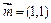 ,向量
,向量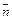 与向量
与向量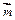 夹角为
夹角为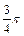 ,且
,且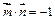 .(1)求向量
.(1)求向量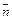 ;(2)若向量
;(2)若向量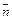 与向量
与向量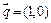 的夹角为
的夹角为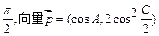 ,其中
,其中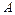 ,B,
,B,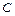 为
为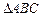 的内角,且
的内角,且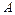 ,
,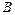 ,
,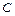 依次成等差数列,试求|
依次成等差数列,试求|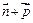 |的取值范围。
|的取值范围。
已知函数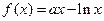
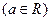 ,
,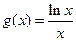 ,其中
,其中 (1)若
(1)若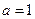 ,求
,求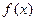 的极小值;(2)在(1)条件下证明
的极小值;(2)在(1)条件下证明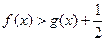 ;(3)是否存在实数
;(3)是否存在实数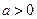 ,使
,使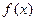 的最小值为3,如果存在,求出实数
的最小值为3,如果存在,求出实数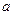 的值,若不存在,说明理由.
的值,若不存在,说明理由.
在 中,
中,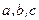 分别是角A、B、C的对边,
分别是角A、B、C的对边, 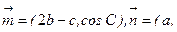
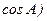 ,且
,且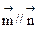 .(1)求角A的大小;(2)求
.(1)求角A的大小;(2)求 的值域.
的值域.