已知f(x)=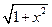 定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
定义在区间[-1,1]上,设x1,x2∈[-1,1]且x1≠x2.
求证: | f(x1)-f(x2)|≤| x1-x2|
 已知二阶矩阵A的属于特征值-1的一个特征向量为,属于特征值3的一个特征向量为,求矩阵A.
已知二阶矩阵A的属于特征值-1的一个特征向量为,属于特征值3的一个特征向量为,求矩阵A.
)函数 .
.
求证:不等式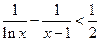 对于
对于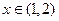 恒成立
恒成立
如图所示,一条直角走廊宽为2米。现有一转动灵活的平板车,其平板面为矩形ABEF,它的宽为1米。直线EF分别交直线AC、BC于M、N,过墙角D作DP⊥AC于P,DQ⊥BC于Q;若平板车要想顺利通过直角走廊,其长度不能超过多少米?
一个四棱锥的三视图和直观图如图所示,E为侧棱PD的中点.
(1)求证:PB//平面AEC;
 (2)若F为侧棱PA上的一点,且
(2)若F为侧棱PA上的一点,且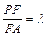 , 则为何值时,PA平面BDF? 并求此时几何体F—BDC的体积.
, 则为何值时,PA平面BDF? 并求此时几何体F—BDC的体积.