(文)经观测,一卫星环绕某行星做圆形轨道运动的半径为r,周期为T,若卫星质量为m.求:(1)卫星向心加速度的大小 (2)行星的质量;
放在光滑水平面上的物体A和B之间用一个弹簧相连,一颗水平飞行的子弹沿着AB连线击中A,并留在其中,若A、B、子弹质量分别为mA、mB、m,子弹击中A之前的速度为v0,要求求解以后过程中弹簧的最大弹性势能。
某同学给出了如下的解题过程:
三者速度相等时弹性势能最大,由动量守恒得: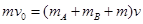
还列出了能量守恒方程: 
并据此得出结论。你认为这位同学的解题过程正确吗?
如正确,请求出最大弹性势能的表达式;如果错误,请你书写正确的求解过程并解出最大弹性势能.
已知氢原子基态的电子轨道为r1=0.528×10-10 m,量子数为n的能级值为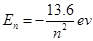
(1)求电子在基态轨道上运动时的动能.
(2)有一群氢原子处于量子数n=3的激发态.在图上用箭头标明这些氢原子能发出哪几条光谱线.
(3)计算这几条光谱线中波长最短的一条的波长(第三问保留一位有效数字).
(其中静电力恒量k=9.0×109 N·m2/C2,电子电量e=1.6×10-19 C,普朗克恒量h=6.63×10-34 J·s,真空中光速c=3.0×108 m/s)
如图所示,AB为固定在竖直平面内的 光滑圆弧轨道,轨道的B点与水平地面相切,其半径为R.质量为m的小球由A点静止释放,求:
光滑圆弧轨道,轨道的B点与水平地面相切,其半径为R.质量为m的小球由A点静止释放,求:
(1)小球滑到最低点B时,小球速度v的大小及小球对轨道的压力F压的大小;
(2)小球通过光滑的水平面BC滑上固定曲面,恰达最高点D,D到地面的高度为h(已知h<R),则小球在曲面上克服摩擦力所做的功Wf.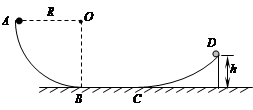
如图所示,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg,现给小球一初速度使它做圆周运动。
(1)若小球通过轨道最高点a处的速度为v1=1m/s时,求球对细杆作用力;
(2)若小球通过轨道最高点a处的速度为v2=3m/s时,求球对细杆作用力。(g=10m/s2)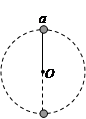
在5m高处以10m / s 的速度水平抛出一小球,不计空气阻力,g 取 10 m / s2,求:
(1)小球在空中运动的时间;
(2)小球落地时的水平位移大小;
(3)小球落地时的速度大小。