九（3）班“2012年新年联欢会”中，有一个摸奖游戏，规则如下：有4张纸牌，背面都是喜羊羊头像，正面有2张笑脸、 2张哭脸．现将4张纸牌洗匀后背面朝上摆放到桌上，然后让同学去翻纸牌．
（1）现小芳有一次翻牌机会，若正面是笑脸的就获奖，正面是哭脸的不获奖．她从中随机翻开一张纸牌，小芳获奖的概率是 ．
（2）如果小芳、小明都有翻两张牌的机会．小芳先翻一张，放回后再翻一张；小明同时翻开两张纸牌．他们翻开的两张纸牌中只要出现笑脸就获奖．他们获奖的机会相等吗？通过树状图分析说明理由．
（本题共两小题，每小题6分，满分12分）
（1）计算：
．
（2）解不等式组
在平面直角坐标系中，抛物线经过O（0，0）、
A（4，0）、B（3，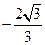
）三点.
（1）求此抛物线的解析式；
（2）以OA的中点M为圆心，OM长为半径作⊙M，在（1）中的抛物线上是否存在这样的点P，过点P作⊙M的切线l ，且l与x轴的夹角为30°，若存在，请求出此时点P的坐标；若不存在，请说明理由.（注意：本题中的结果可保留根号）
已知反比例函数y＝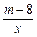
(m为常数)的图象经过点A（－1，6）．
（1）求m的值；
（2）如图，过点A作直线AC与函数y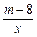＝的图象交于点B，与x轴交于点C，且AB＝2BC，求点C的坐标．
小莉的爸爸买了2010年7月份去上海看世博会的一张门票，她和哥哥两人都很想去观看，可门票只有一张，读九年级的哥哥想了一个办法，拿了八张扑克牌，将数字为1，2，3，5的四张牌给小莉，将数字为4，6，7，8的四张牌留给自己，并按如下游戏规则进行：小莉和哥哥从各自的四张牌中随机抽出一张，然后将抽出的两张扑克牌数字相加，如果和为偶数，则小莉去；如果和为奇数，则哥哥去．
（1）请用数状图或列表的方法求小莉去上海看世博会的概率；
（2）哥哥设计的游戏规则公平吗？若公平，请说明理由；若不公平，请你设计一种公平的游戏规则．
杭州所前“杨梅节”期间，某中学70名教职工组团前往参观欣赏，旅游景点规定：①门票每人60元，无优惠；②上山游玩可坐景点观光车，观光车有四座和十一座车，四座车每辆60元，十一座车每人10元.学校教职工正好坐满每辆车且总费用不超过5000元，问学校租用的四座车和十一座车各多少辆？