如图,学校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
|
甲 |
8 |
9 |
7 |
9 |
8 |
6 |
7 |
8 |
10 |
8 |
|
乙 |
6 |
7 |
9 |
7 |
9 |
10 |
8 |
7 |
7 |
10 |
且 =8,S乙2=1.8,根据上述信息完成下列问题:
=8,S乙2=1.8,根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是 ,中位数是 .
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.

如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.

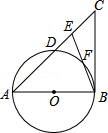
如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
某地区2014年投入教育经费2900万元,2016年投入教育经费3509万元.
(1)求2014年至2016年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的增长情况,该地区到2018年需投入教育经费4250万元,如果按(1)中教育经费投入的增长率,到2018年该地区投入的教育经费是否能达到4250万元?请说明理由.
(参考数据: )
如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB= ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
