如图,平面直角坐标系中O为坐标原点,直线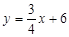 与x轴、y轴分别交于A、B两点,C为OA中点;
与x轴、y轴分别交于A、B两点,C为OA中点;
(1)求直线BC解析式;
(2)动点P从O出发以每秒2个单位长度的速度沿线段OA向终点A运动,同时动点Q从C出发沿线段CB以每秒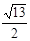 个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;
个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;
(3)在(2)的条件下,以PC为直径作⊙N,求t为何值时直线QM与⊙N相切.
(本题12分)如图,抛物线 与x轴交于A、B两点,与y轴交于C点.
与x轴交于A、B两点,与y轴交于C点.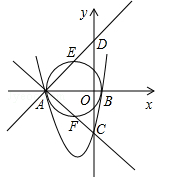
(1)求抛物线的顶点坐标;
(2)设直线 与y轴的交点是D,在线段AD上任意取一点E(不与A、D重合),经过A、B、E三点的圆交直线AC于点F,试判断△BEF的形状,并说明理由.
与y轴的交点是D,在线段AD上任意取一点E(不与A、D重合),经过A、B、E三点的圆交直线AC于点F,试判断△BEF的形状,并说明理由.
(本题10分)某商品的进价为每件30元,现在的售价为每件40元,每星期可卖出150件.市场调查反映:如果每件的售价每涨1元(售价每件不能高于45元),那么每星期少卖10件.设每件涨价x元(x为非负整数),每星期的销量为y件.
(1)求y与x的函数关系式及自变量x的取值范围;
(2)如何定价才能使每星期的利润最大且每星期的销量较大?每星期的最大利润是多少?
(本题8分)如图1,在一个不透明的袋子中装有四个球,分别标有字母A、B、C、D,这些球除了字母外完全相同,此外,有一面白色、另一面黑色、大小相同的四张正方形卡片,每张卡片两面的字母相同,分别标有字母A、B、C、D.最初,摆成如图2的样子,A.D是黑色,B.C是白色.
两次操作后观察卡片的颜色.
(如:第一次取出A、第二次取出B,此时卡片的颜色变成 )
)
(1)求取四张卡片变成相同颜色的概率;
(2)求四张卡片变成两黑两白、并恰好形成各自颜色的矩形的概率.
(本题8分)如图,AB是⊙O的直径,C.D两点在⊙O上,若∠C=45°.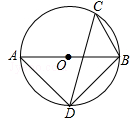
(1)求∠ABD的度数;
(2)若∠CDB=30°,BC=3,求⊙O的半径.
(本题8分)一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为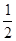 .
.
(1)布袋里红球有多少个?
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率.