(本题10分)某商品的进价为每件30元,现在的售价为每件40元,每星期可卖出150件.市场调查反映:如果每件的售价每涨1元(售价每件不能高于45元),那么每星期少卖10件.设每件涨价x元(x为非负整数),每星期的销量为y件.
(1)求y与x的函数关系式及自变量x的取值范围;
(2)如何定价才能使每星期的利润最大且每星期的销量较大?每星期的最大利润是多少?
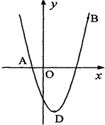
如图①已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转。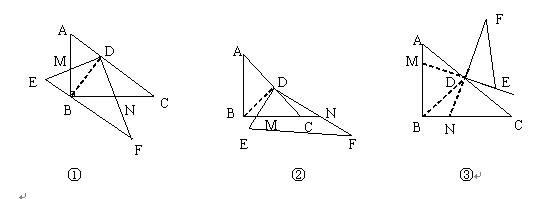
在图①中,DE交AB于M,DF交BC于N,①证明:DM=DN;②在这一过程中,直角三角板DEF与△ABC的重叠部分DMBN,请说明四边形DMBN的面积是否发生变化,若发生变化,请说明四边形DMBN如何变化。若不变,求其面积。
继续旋转至如图②延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立请给出证明;若不成立,请说明理由
继续转至图③延长FD交BC于N延长ED交AB于M,DM=DN是否仍然成立?若成立请直接写出结论,不用证明。
如图,在△ABC中,E、F分别是AB、AC上的点。
①AD平分∠BAC;②DE⊥AB,DF⊥AC;③AD⊥EF以其中的两个为条件,另一个为结论,可构成三个命题,即⑴①②→③;⑵①③→②;⑶②③→①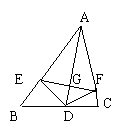
试判断上述三个命题是否正确。
请证明你认为正确的命题
某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.

请你根据图表中的信息回答下列问题:求选择长跑训练的人数占全班人数的百分比及该班学生的总人数;
求训练后篮球定时定点投篮人均进球数
根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%。请求出参加训练之前的人均进球数。
在一堂数学课中,数学老师给出了如下问题“已知:如图①,在四边形ABCD中,AB=AD,∠B=∠D.求证:CB=CD”.文文和彬彬都想到了利用辅助线把四边形的问题转化为三角形来解决.
文文同学证明过程如下:连结AC(如图②)
∵∠B=∠D ,AB=AD,AC=AC
∴△ABC≌△ADC,∴CB=CD
你认为文文的证法是的.(在横线上填写“正确”或“错误”)彬彬同学的辅助线作法是“连结BD”(如图③),请完成彬彬同学的证明过程.
如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请
解答下列问题:求抛物线的解析式;
若抛物线的顶点为点D,对称轴所在的直线交x轴于点E,连接AD,点F为AD的中点,求出线段EF的长。
注:抛物线y=ax2+bx+c的对称轴是x=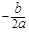 ,顶点坐标是(
,顶点坐标是(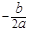 ,
,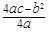 )。
)。