如图所示,O为坐标原点,过点P(2,0)且斜率为k的直线L交抛物线y =2x于M(x
=2x于M(x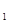 ,y
,y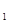 ),N(x
),N(x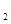 ,y
,y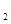 )两点. ⑴写出直线L的方程;⑵求x
)两点. ⑴写出直线L的方程;⑵求x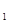 x
x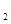 与y
与y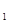 y
y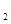 的值;⑶求证:OM⊥ON
的值;⑶求证:OM⊥ON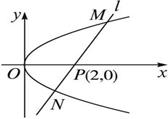
已知过点P(1,-2),倾斜角为 的直线
的直线 和抛物线x2="y+m" ,
和抛物线x2="y+m" ,
(1)m取何值时,直线 和抛物线交于两点?
和抛物线交于两点?
(2)m取何值时,直线 被抛物线截下的线段长为
被抛物线截下的线段长为 .
.
已知曲线C的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴, 建立平面直角坐标系,直线
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴, 建立平面直角坐标系,直线 的参数方程是:
的参数方程是: (
( 是参数).
是参数).
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,将直线 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)若直线 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且 ,试求实数m值.
,试求实数m值.
已知直线 经过点
经过点 ,倾斜角
,倾斜角 。
。
(1)写出直线 的参数方程;
的参数方程;
(2)设 与圆
与圆 相交于两点
相交于两点 、
、 ,求点
,求点 到
到 、
、 两点的距离之和。
两点的距离之和。
(本小题满分12分)
已知定义域为 的函数
的函数 满足:①
满足:① 时,
时, ;②
;② ③对任意的正实数
③对任意的正实数 ,都
,都
有 .
.
(1)求证: ;
;
(2)求证: 在定义域内为减函数;
在定义域内为减函数;
(3)求不等式 的解集.
的解集.
(本小题满分12分)
已知定义在R上奇函数 在
在 时的图象是如图所示的抛物线的一部分.
时的图象是如图所示的抛物线的一部分.
(1)请补全函数 的图象;
的图象;
(2)写出函数 的表达式(只写明结果,无需过程);
的表达式(只写明结果,无需过程);
(3)讨论方程 的解的个数(只写明结果,无需过程).
的解的个数(只写明结果,无需过程).