如图，抛物线C1：y=ax2+bx+1的顶点坐标为D（1，0），
（1）求抛物线C1的解析式；
（2）如图1，将抛物线C1向右平移1个单位，向下平移1个单位得到抛物线C2，直线y=x+c，经过点D交y轴于点A，交抛物线C2于点B，抛物线C2的顶点为P，求△DBP的面积；
（3）如图2，连接AP，过点B作BC⊥AP于C，设点Q为抛物线上点P至点B之间的一动点，连接PQ并延长交BC于点E，连接BQ并延长交AC于点F，试证明：FC·（AC+EC）为定值．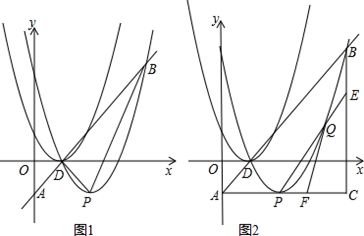
如图，等腰△OAB在直角坐标系中的位置如图，点A的坐标为（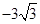
，3），点B的坐标为（-6，0）.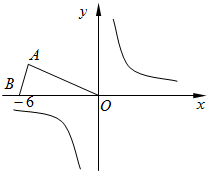
（1）若△OAB关于y轴的轴对称图形是三角形OA′B′，请直接写出A、B的对称点A′、B′的坐标；
（2）若将三角形OAB沿x轴向右平移a个单位，此时点A恰好落在反比例函数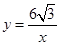
的图像上，求a的值；
（3）若△OAB绕点O按逆时针方向旋转α度（0＜α＜900）．
①当α=30°时点B恰好落在反比例函数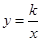
的图象上，求k的值；
②问点A、B能否同时落在①中的反比例函数的图象上，若能，求出α的值；若不能，请说明理由．
如图，正方形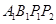
的顶点
、
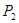在反比例函数
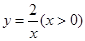的图象上，顶点
、
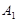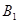分别在
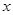轴、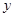
轴的正半轴上，再在其右侧作正方形
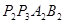，顶点
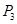在反比例函数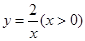的图象上，顶点
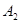在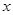轴的正半轴上，则点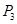的坐标为 ．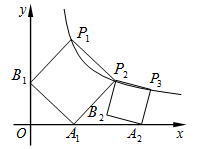
某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系：
| X（元） |
3 |
4 |
5 |
6 |
| y（个） |
20 |
15 |
12 |
10 |
（1）根据表中的数据在平面直角坐标系中描出实数对（x,y）的对应点．
（2）猜测并确定y与x之间的函数关系式，并画出图象；
（3）设经营此贺卡的销售利润为w元，试求出w与x之间的函数关系式，若物价局规定此贺卡的销售价最高不能超过10元／个，请你求出当日销售单价x定为多少元时，才能获得最大日销售利润？
将油箱注满k升油后，轿车可行驶的总路程S（单位：千米）与平均耗油量a（单位：升/千米）之间是反比例函数关系S=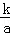
（k是常数，k≠0）．已知某轿车油箱注满油后，以平均耗油量为每千米耗油0.1升的速度行驶，可行驶700千米．
（1）求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式（关系式）；
（2）当平均耗油量为0.08升/千米时，该轿车可以行驶多少千米？
如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数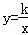
（k≠0）在第一象限内的图象经过点D、E，且D点的横坐标是它的纵坐标的2倍．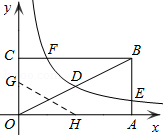
（1）求边AB的长；
（2）求反比例函数的解析式和n的值；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．