如图,等腰△OAB在直角坐标系中的位置如图,点A的坐标为(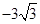 ,3),点B的坐标为(-6,0).
,3),点B的坐标为(-6,0).
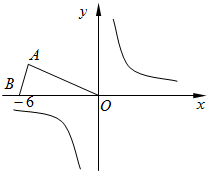
(1)若△OAB关于y轴的轴对称图形是三角形OA′B′,请直接写出A、B的对称点A′、B′的坐标;
(2)若将三角形OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数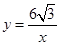 的图像上,求a的值;
的图像上,求a的值;
(3)若△OAB绕点O按逆时针方向旋转α度(0<α<900).
①当α=30°时点B恰好落在反比例函数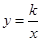 的图象上,求k的值;
的图象上,求k的值;
②问点A、B能否同时落在①中的反比例函数的图象上,若能,求出α的值;若不能,请说明理由.
如图,在路灯下,电线杆AB的影子是AB′,电线杆CD的影子是CD′,请你在图中确定光源的位置,并画出电线杆EF的影子.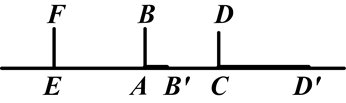
两根竹竿如图①所示直立在地面上,竹竿甲的影子为AB,请在图中画出形成影子AB的太阳光线,并画出同一时刻竹竿乙的影子.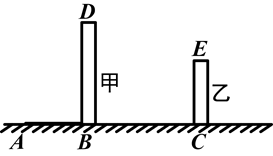
为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡AB的长为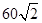 米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
(1)若修建的斜坡BE的坡比为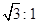 ,求休闲平台DE的长.
,求休闲平台DE的长.
(2)一座建筑物距离A点33米远(即AG=33米),小亮在D点处测得建筑物顶部H的仰角(即∠HDM)为30°.点B,C,A,G,H在同一个平面内,点C,A,G在同一条直线上,且HG⊥CG.问:建筑物的高GH为多少米?
某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校旗杆的高,小明站在点B处测得旗杆顶端E点的仰角为45°,小军站在点D处测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF.(结果精确到0.1米,参考数据: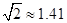 ,
,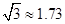 )
)
为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形。
活动中测得的数据如下:
①小明的身高DC=1.5m;
②小明的影长CE=1.7m;
③小明的脚到旗杆底部的距离BC=9m;
④旗杆的影长BF=7.6m;
⑤从D点看A点的仰角为30°.
请选择你需要的数据,求出旗杆的高度.(计算结果精确到0.1m,参考数据: ,
,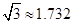 )
)