菲尔兹奖（Fields Medal）是享有崇高声誉的数学大奖，每四年颁奖一次，颁给二至四名成就显著的年轻数学家．获奖者当年不能超过四十岁．对获奖者获奖时的年龄进行统计，整理成下面的表格和统计图．
| 年龄段（岁） |
27≤x＜29 |
29≤x＜31 |
31≤x＜33 |
33≤x＜35 |
35≤x＜37 |
37≤x＜39 |
39≤x＜41 |
| 频数（人） |
1 |
2 |
7 |
5 |
a |
b |
c |
| 频率 |
0．025 |
|
|
|
0．175 |
|
0．15 |
（1）直接写出a、b、c的值，并补全条形统计图；
（2）请问这组数据的中位数在哪一个年龄段中？
（3）在五位36岁的获奖者中有两位美国人，一位法国人和两位俄罗斯人．请用画树形图或列表的方法求出“从五位36岁的获奖者中随机抽出两人，刚好是不同国籍的人”（记作事件A）的概率．
如图①，一条笔直的公路上有A、B、C三地，B、C两地相距 150 千米，甲、乙两辆汽车分别从B、C两地同时出发，沿公路匀速相向而行，分别驶往C、B两地．甲、乙两车到A地的距离
、
（千米）与行驶时间 x（时）的关系如图②所示． 
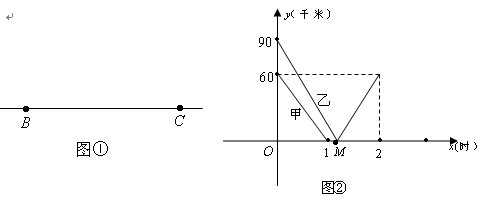
根据图象进行以下探究： （1）请在图①中标出 A地的位置，并作简要说明；
(2) 甲的速度为
，乙的速度为.（3）求图②中M点的坐标，并解释该点的实际意义；
（4）在图②中补全甲车到达C地的函数图象，求甲车到 A地的距离
与行驶时间x的函数关系式；（5）出发多长时间，甲、乙两车距A点的距离相等？
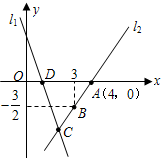
如图，直线l1的解析表达式为：
，且l1与x轴
交于点D，直线l2经过点A，B，直线l1，l2交于点C．（1）求直线l2的函数关系式；
（2）求△ADC的面积；
（3）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、D、C、H为顶点的四边形是平行四边形？若存在，请直接写出点H的坐标；若不存在，请说明理由．
(本题满分10分) 把两个三角形按如图1放置，其中∠ACB=∠DEC=90°，
∠CAB=45°，∠CDE=30°，且AB=12，DC=14，把△DCE绕点C顺时针旋转15°
得△D1CE1，如图2，这时AB与CD1相交于点O、与D1E1相交于点F；
（1）求∠AC D1的度数；
（2）求线段AD1的长.
某通讯公司推出①、②两种通讯收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的收费y（元）与通讯时间x（分钟）之间的函数关系如图所示．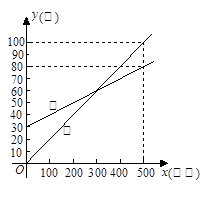
（1）有月租费的收费方式是（填①或②），月租费是元；
（2）分别求出①、②两种收费方式中收费y（元）与通讯时间x（分钟）之间的函数关系式；
（3）请你根据用户通讯时间的多少，给出经济实惠的选择建议．
如图，四边形ABCD为直角梯形
，AD‖BC，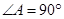
，
，
．
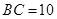动点P、Q分别从A、C两点同时出发，点P以每秒1个单
位的速度由A向D运动，点Q以每秒2个单位的速度由C向B运动，当点Q停
止运动时，点P也停止运动，设运动时间为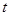
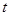（0≤≤5），
（1）当t为多少时，四边形PQCD是平行四边形？
（2）当t为多少时，四边形PQCD是等腰梯形？