如图,A市气象站测得台风中心在A市正东方向300千米的B处,以10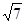 千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
(1)A市是否会受到台风的影响?写出你的结论并给予说明;
(2)如果A市受这次台风影响,那么受台风影响的时间有多长?
有一项工程,若甲队单独做,恰好在规定日期完成,若乙队单独做要超过规定日期3天完成;现在先由甲、乙两队合做2天后,剩下的工程再由乙队单独做,也刚好在规定日期完成,问规定日期多少天?
如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算蔬菜的产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°.请你和小明一起来求这块土地的面积.
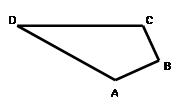 |
一种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
解方程:  .
.