(本小题满分13分)已知数列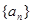 的前
的前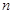 项和
项和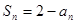 ,数列
,数列 满足
满足 ,且
,且 (
(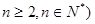 .
.
(Ⅰ)求数列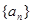 和
和 的通项公式;
的通项公式;
(Ⅱ)若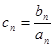 ,求数列
,求数列 的前
的前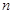 项和
项和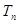 .
.
(本小题满分13分)如图,在直三棱柱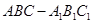 中,
中,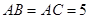 ,
,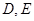 分别为
分别为 的中点,四边形
的中点,四边形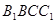 是边长为
是边长为 的正方形.
的正方形.
(Ⅰ)求证: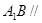 平面
平面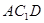 ;
;
(Ⅱ)求证: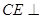 平面
平面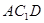 ;
;
(Ⅲ)求二面角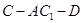 的余弦值.
的余弦值.
(本小题满分13分)已知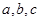 分别为
分别为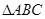 的三个内角
的三个内角 的对边,满足
的对边,满足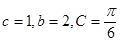 .
.
(Ⅰ)求 及
及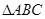 的面积;
的面积;
(Ⅱ)设函数 ,其中
,其中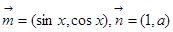 ,求
,求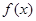 的值域.
的值域.
已知二次函数 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在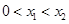 ,使得不等式
,使得不等式 成立,设数列
成立,设数列 的前
的前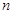 项和
项和 。
。
(1)求函数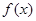 的表达式;
的表达式;
(2)求数列 的通项公式;
的通项公式;
(3)设各项均不为 的数列
的数列 中,所有满足
中,所有满足 的整数
的整数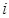 的个数称为这个数列
的个数称为这个数列 的变号数,令
的变号数,令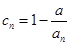 (
(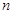
 ),求数列
),求数列 的变号数.
的变号数.
已知数列 ,其前
,其前 项和
项和 满足
满足 是大于0的常数),且
是大于0的常数),且
(1)求 的值;
的值;
(2)求数列 的通项公式an;
的通项公式an;
(3)设数列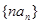 的前n项和为Tn,试比较
的前n项和为Tn,试比较 与Sn的大小.
与Sn的大小.