某商场经营某种品牌的童装，购进时的单价是60元．根据市场调查，在一段时间内，销售单价是80元时，销售量是200件，而销售单价每降低1元，就可多售出20件．
（1）写出销售量y（件）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，商场销售该品牌童装获得的利润为4000元？
（3）若童装厂规定该品牌童装销售单价不低于76元，则商场销售该品牌童装获得的最大利润是多少？
已知抛物线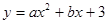
经过点A（－1，0），B（3，0），交
轴于点C，M为抛物线的顶点，连接MB．
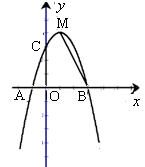
（1）求该抛物线的解析式；
（2）在轴上是否存在点P满足△PBM是直角三角形，若存在，请求出P点的坐标，若不存在，请说明理由；
（3）设Q点的坐标为（8，0），将该抛物线绕点Q旋转180°后，点M的对应点为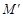
，求
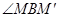的度数．
如图，AB是半圆O的直径，且AB＝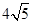
，矩形CDEF内接于半圆，点C，D在AB上，点E，F在半圆上．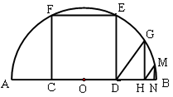
（1）当矩形CDEF相邻两边FC︰CD＝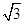
︰2时，求弧AF的度数；
（2）当四边形CDEF是正方形时：
①试求正方形CDEF的边长；
②若点G，M在⊙O上， GH⊥AB于H，MN⊥AB于N，且△GDH和△MHN都是等腰直角三角形，求HN的长．
如图，两个观察者从A，B两地观测空中C处一个气球，分别测得仰角为45º和60º．已知A，B两地相距30米，延长AB，作CD⊥AD于D，当气球沿着与AB平行的方向飘移到点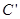
时，在A处又测得气球的仰角为30º，求CD与
的长度．（结果保留根号）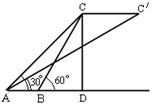
已知在平面直角坐标系中，点A，B的坐标分别为A（2，－5），
B（5，1）．在同一个坐标系内画出满足下列条件的点（保留画图痕迹），并求出该点的坐标．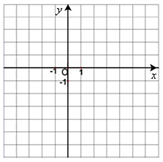
（1）在
轴上找一点C，使得AC＋BC的值最小；
（2）在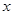
轴上找一点D，使得AD－BD的值最大．
有六张正面分别有数字－3，－1，0，1，5，6的不透明卡片，它们除数字不同外其余全部相同．现将它们背面向上，洗匀后从中任取一张，将该卡片上的数字记为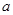
，求关于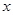
的分式方程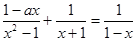
的解，并求该方程的解不小于
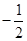的概率．