已知椭圆的两个焦点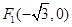 ,
, ,过
,过 且与坐标轴不平行的直线
且与坐标轴不平行的直线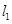 与椭圆交于
与椭圆交于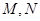 两点,如果
两点,如果 的周长等于8。
的周长等于8。
(1)求椭圆的方程;
(2)若过点 的直线
的直线 与椭圆交于不同两点
与椭圆交于不同两点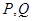 ,试问在
,试问在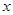 轴上是否存在定点
轴上是否存在定点 ,使
,使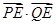 恒为定值?若存在,求出点
恒为定值?若存在,求出点 的坐标及定值;若不存在,说明理由。
的坐标及定值;若不存在,说明理由。
已知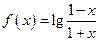 ,
,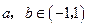 求证:
求证: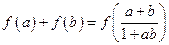 .
.
已知 为正数,
为正数, ,且
,且 ,求证:
,求证: .
.
20世纪30年代,里克特制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大.这就是我们常说的里氏震级 ,其计算公式为
,其计算公式为 ,其中,
,其中, 是被测地震的最大振幅,
是被测地震的最大振幅, 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).
(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅
是20,此时标准地震的振幅是 ,计算这次地震的震级(精确到
,计算这次地震的震级(精确到 );
);
(2)5级地震给人的震感已比较明显,计算 级地震的最大振幅是5级地震
级地震的最大振幅是5级地震
的最大振幅的多少倍(精确到1).
已知函数 在区间
在区间 上恒为正值,
上恒为正值,
求实数 的取值范围.
的取值范围.
若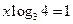 ,求
,求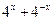 的值.
的值.