某校为了解高二学生 、
、 两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关, 随机抽取了该年级一次期末考试 、
、 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2 2列联表:
2列联表:
| |
 学科合格人数 学科合格人数 |
 学科不合格人数 学科不合格人数 |
合计 |
 学科合格人数 学科合格人数 |
40 |
20 |
60 |
 学科不合格人数 学科不合格人数 |
20 |
30 |
50 |
| 合计 |
60 |
50 |
110 |
(1)据此表格资料,你认为有多大把握认为“ 学科合格”与“
学科合格”与“ 学科合格”有关;
学科合格”有关;
(2)从“ 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“ 学科合格”的人数为
学科合格”的人数为 ,求
,求 的数学期望.
的数学期望.
附公式与表:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
(本题13分)已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,PA⊥平面ABCD.
(1)求证:PF⊥FD;
(2)设点G在PA上,且EG//平面PFD,试确定点G的位置.
(本小题满分13分)数列{ }的前
}的前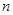 项和为
项和为 ,
, 是
是 和
和 的等差中项,等差数列{
的等差中项,等差数列{ }满足
}满足 ,
, .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前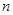 项和
项和
(本题10分)已知直线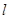 的方程为
的方程为 ,
,
(1)若直线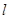 的斜率是
的斜率是 ;求
;求 的值;
的值;
(2)若直线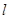 在
在 轴、
轴、 轴上的截距之和等于
轴上的截距之和等于 ;求
;求 的值;
的值;
(3)求证:直线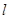 恒过定点。
恒过定点。
(本小题满分10分)在三角形ABC中,∠A,∠B,∠C的对边分别为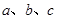 且
且
(1)求∠A;
(2)若 ,求
,求 的取值范围.
的取值范围.
已知各项均为正数的数列 的前
的前 项和为
项和为 ,且
,且 ,
,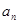 ,
, 成等差数列,
成等差数列,
(1)求数列 的通项公式;
的通项公式;
(2)若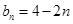
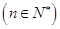 ,设
,设 ,求数列
,求数列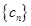 的前
的前 项和
项和