(本题13分)已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,PA⊥平面ABCD.
(1)求证:PF⊥FD;
(2)设点G在PA上,且EG//平面PFD,试确定点G的位置.
如图,
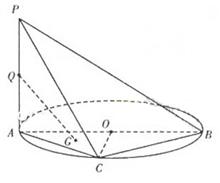
(Ⅰ)求证: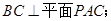
(Ⅱ)设
已知两定点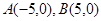 ,
,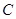 为动点
为动点
(1)若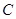 在x轴上方,且
在x轴上方,且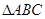 是等腰直角三角形,求
是等腰直角三角形,求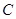 点坐标;
点坐标;
(2)若直线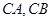 的斜率乘积为
的斜率乘积为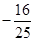 ,求
,求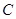 点坐标
点坐标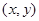 满足的关系式。
满足的关系式。
已知直线l:3x-y+3=0,求:
(1)过点P(4,5)且与直线l垂直的直线方程;
(2)与直线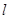 平行且距离等于
平行且距离等于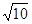 的直线方程。
的直线方程。
已知无穷数列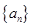 的前
的前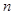 项和为
项和为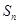 ,且满足
,且满足 ,其中
,其中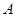 、
、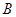 、
、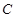 是常数.
是常数.
(1)若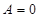 ,
,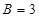 ,
,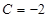 ,求数列
,求数列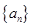 的通项公式;
的通项公式;
(2)若 ,
,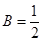 ,
, ,且
,且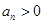 ,求数列
,求数列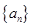 的前
的前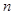 项和
项和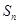 ;
;
(3)试探究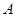 、
、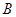 、
、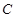 满足什么条件时,数列
满足什么条件时,数列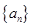 是公比不为
是公比不为 的等比数列.
的等比数列.
已知函数 .
.
(1)若 ,当
,当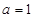 时,求
时,求 的取值范围;
的取值范围;
(2)若定义在 上奇函数
上奇函数 满足
满足 ,且当
,且当 时,
时, ,求
,求 在
在 上的反函数
上的反函数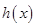 ;
;
(3)若关于 的不等式
的不等式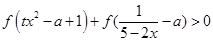 在区间
在区间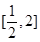 上有解,求实数
上有解,求实数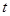 的取值范围.
的取值范围.