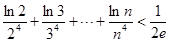某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对 表示“甲在
表示“甲在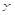 号车站下车,乙在
号车站下车,乙在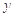 号车站下车”
号车站下车”
(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率.
用四种不同的颜色给3个不同矩形随机涂色,每个矩形只涂一种颜色.
求:(1)3个矩形颜色都相同的概率;
(2)3个矩形颜色都不同的概率;
(3)3个矩形有两个颜色相同的概率
如图,边长为2的等边 所在的平面垂直于矩形
所在的平面垂直于矩形 所在的平面,
所在的平面, ,
, 为
为 的中点.
的中点.
(1)证明: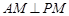 ;
;
(2)求异面直线 和
和 所成角的余弦值.
所成角的余弦值.
设实数 满足
满足 .
.
(1)求 ;(2)求展开式中含
;(2)求展开式中含 项的系数
项的系数
已知椭圆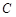 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线 与椭圆
与椭圆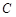 在第一象限内的交点是
在第一象限内的交点是 ,点
,点 在
在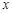 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆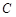 的右焦点
的右焦点 ,椭圆
,椭圆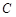 另一个焦点是
另一个焦点是 ,且
,且
(1)求椭圆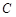 的方程;
的方程;
(2)直线 过点
过点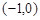 ,且与椭圆
,且与椭圆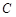 交于
交于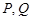 两点,求
两点,求 的内切圆面积的最大值
的内切圆面积的最大值
已知函数
(Ⅰ)求函数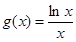 的单调区间;
的单调区间;
(Ⅱ)若不等式 在区间
在区间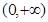 上恒成立,求实数k的取值范围;
上恒成立,求实数k的取值范围;
(Ⅲ)求证: