一边长为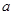 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为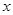 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。
(1)试把方盒的容积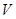 表示为
表示为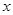 的函数;
的函数;
(2)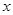 多大时,方盒的容积
多大时,方盒的容积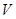 最大?
最大?
(本小题满分15分)已知数列 的前n项和为Sn,且满足Sn+an=2.
的前n项和为Sn,且满足Sn+an=2.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求满足不等式 的n的取值范围.
的n的取值范围.
(本小题满分14分)在 中,角
中,角 、B、C所对的边分别是
、B、C所对的边分别是 ,
, .
.
(Ⅰ)求角C;
(Ⅱ)若 的最短边长是
的最短边长是 ,求最长边的长.
,求最长边的长.
(本题10分)已知 是定义在
是定义在 上的奇函数,
上的奇函数,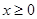 时,
时,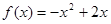 .
.
(1)求 在
在 上的表达式;
上的表达式;
(2)令 ,问是否存在大于零的实数
,问是否存在大于零的实数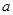 、
、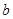 ,使得当
,使得当 时,函数
时,函数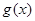 值域为
值域为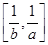 ,若存在求出
,若存在求出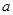 、
、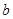 的值,若不存在请说明理由.
的值,若不存在请说明理由.
(本题8分)设二次 ,不等式
,不等式 的解集是
的解集是 .
.
(1)求 ;
;
(2)当函数 的定义域是
的定义域是 时,求函数
时,求函数 的最大值
的最大值 .
.
(本题8分)已知函数 .
.
(1)用单调性定义证明函数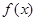 在
在 上是减函数;
上是减函数;
(2)判断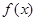 在
在 上的单调性(无需证明);
上的单调性(无需证明);
(3)若函数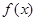 在
在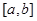 上的值域是
上的值域是 ,求
,求 的最大值和最小值.
的最大值和最小值.