(本题10分)已知 是定义在
是定义在 上的奇函数,
上的奇函数,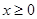 时,
时,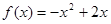 .
.
(1)求 在
在 上的表达式;
上的表达式;
(2)令 ,问是否存在大于零的实数
,问是否存在大于零的实数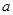 、
、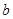 ,使得当
,使得当 时,函数
时,函数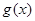 值域为
值域为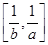 ,若存在求出
,若存在求出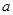 、
、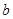 的值,若不存在请说明理由.
的值,若不存在请说明理由.
设正有理数x是 的一个近似值,令
的一个近似值,令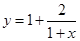 .
.
(Ⅰ)若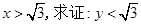 ;
;
(Ⅱ)比较y与x哪一个更接近于 ,请说明理由.
,请说明理由.
在直角坐标系xOy中,圆C的参数方程 为参数).以O为极点,
为参数).以O为极点,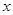 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆C的交点为O,P,与直线
与圆C的交点为O,P,与直线 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
如图,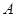 、
、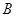 、
、 是圆
是圆 上三点,
上三点,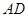 是
是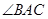 的角平分线,交圆
的角平分线,交圆 于
于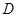 ,过
,过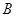 作圆
作圆 的切线交
的切线交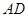 的 延长线于
的 延长线于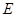 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求证: .
.
已知函数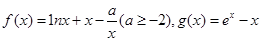 ,其中e为自然对数的底数,且当x>0时
,其中e为自然对数的底数,且当x>0时 恒成立.
恒成立.
(Ⅰ)求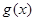 的单调区间;
的单调区间;
(Ⅱ)求实数a的所有可能取值的集合;
(Ⅲ)求证: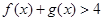 .
.
已知椭圆C长轴的两个顶点为A(-2,0),B(2,0),且其离心率为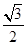 .
.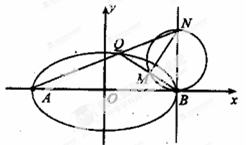
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若N是直线x=2上不同于点B的任意一点,直线AN与椭圆C交于点Q,设直线QB与以NB为直径的圆的一个交点为M(异于点B),求证:直线NM经过定点.