2012年3月25日浙江省环境厅第一次发布七城市PM2．5浓度数据(表一)
2012年3月24日PM2．5监测试报数据
| 城市名称 |
日平均浓度(微克／立方米) |
分指数(IAOI) |
| 杭州 |
35 |
50 |
| 宁波 |
49 |
|
| 温州 |
33 |
48 |
| 湖州 |
40 |
57 |
| 嘉兴 |
33 |
48 |
| 绍兴 |
44 |
|
| 舟山 |
30 |
43 |
(1)已知绍兴和宁波两市的分指数的和是杭州、湖州、舟山三市分指数和的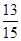
，绍兴分指数的5倍与宁波分指数的3倍的差比温州和嘉兴两市分指数的和大10，求绍兴和宁波两市的分指数；
(2)问上述七城市中分指数的极差是多少?位于中位数的城市是哪一个城市?
(3)描述一组数据的离散程度，我们可以用“极差”、“方差”、“平均差”[平均差公式为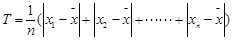
，求杭州，温州，湖州，嘉兴，舟山五个城市中分指数的平均差。
（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点,P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°.
求证：AM=MN．
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连ME．
∵正方形ABCD中，∠B=90°，∠AMN=90°
∴∠1=180°-∠AMN-∠AMB =180°-∠B-∠AMB=∠2
（下面请你完成余下的证明过程）
（2）若将(1)中的“正方形ABCD”改为“正三角形ABC”（如图2）,N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
王华、张伟两位同学九年级10次数学单元自我检测的成绩（成绩均为整数，且个位数为0）分别如下图所示：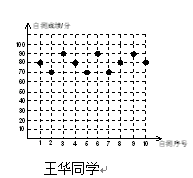
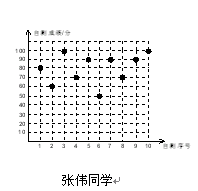
（1）根据上图中提供的数据填写下表：
（2）如果将90分以上（含90分）的成绩视为优秀，则优秀率高的同学是________.
（3）如果要从这两个同学选一位去参加数学竞赛，你可以给老师一些建议吗？
如图，利用一面墙（墙的长度不超过45m），用80m长的篱笆围一个矩形场地．
⑴怎样围才能使矩形场地的面积为750m2?
⑵能否使所围矩形场地的面积为810m2，为什么?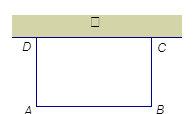
已知，如图，矩形ABCD的对角线AC，BD相交于点O，E，F分别是OA，OB的中点．
（1）求证：△ADE≌△BCF；（2）若AD=4cm，AB=8cm，求OF的长．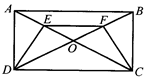
已知y=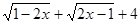
（1）求x， y的值。（2）根据（1）中x，y值，求
的值。