设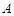 是由
是由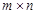 个实数组成的
个实数组成的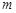 行
行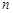 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(Ⅰ) 数表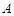 如表所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
如表所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
| 1 |
2 |
3 |
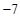 |
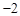 |
1 |
0 |
1 |
(Ⅱ) 数表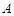 如表所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数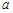 的所有可能值;
的所有可能值;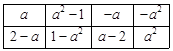
(Ⅲ)对由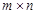 个实数组成的
个实数组成的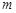 行
行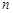 列的任意一个数表
列的任意一个数表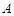 ,
,
能否经过有限次“操作”以后,使得到的数表每行的各数之
和与每列的各数之和均为非负整数?请说明理由.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图像如图所示,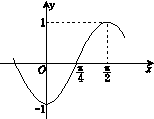
(1)求ω,φ的值;
(2)设g(x)=2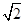 f
f f
f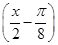 -1,当x∈[0,
-1,当x∈[0,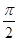 ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.
已知函数f(x)= .
.
(1)求函数f(x)的定义域;
(2)设α是第四象限的角,且tan α=- ,求f(α)的值.
,求f(α)的值.
在△ABC中,内角A,B,C所对的边分别为a,b,c,cos B=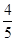 .
.
(1)求cos(A+C)的值;
(2)求sin 的值;
的值;
(3)若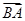 ·
·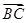 =20,求△ABC的面积.
=20,求△ABC的面积.
在△ABC中,内角A,B,C所对的边分别为a,b,c,且f(A)=2cos 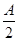 sin
sin +sin2
+sin2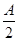 -cos2
-cos2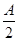 .
.
(1)求函数f(A)的最大值;
(2)若f(A)=0,C= ,a=
,a=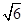 ,求b的值.
,求b的值.
已知函数f(x)=2 sin xcos x+2cos2x+m在区间
sin xcos x+2cos2x+m在区间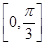 上的最大值为2.
上的最大值为2.
(1)求常数m的值;
(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,若f(A)=1,sin B=3sin C,△ABC的面积为 ,求边长a.
,求边长a.