商场购进某种新商品的每件进价为120元,在试销期间发现,当每件商品的售价为130元时,每天可销售70件;当每件商品的售价高于130元时,每涨价1元,日销售量就减少1件,据此规律,请回答下列问题.
(1)当每件商品的售价为140元时,每天可销售 件商品,商场每天可盈利 元;
(2)设销售价定为x元时,商品每天可销售 件,每件盈
利 元;
(3)在商品销售正常的情况下,每件商品的销售价定为多少元时,商场每天盈利可达到1500元(提示:盈利=售价-进价);
(4)能不能通过适当的降价,使商场的每天盈利达到最大.若能,请求出售价多少元时每天盈利最大,每天最大盈利为多少元(若能,可直接写出答案)?若不能,请说明理由.
已知:如图,O为数轴的原点,A,B分别为数轴上的两点,A点对应的数为-30,B点对应的数为100.
(1)A、B间的距离是;
(2)若点C也是数轴上的点,C到B的距离是C到原点O的距离的3倍,求C对应的数;
(3)若当电子P从B点出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4个单位长度/秒的速度向左运动,设两只电子蚂蚁在数轴上的D点相遇,那么D点对应的数是多少?
(4)若电子蚂蚁P从B点出发,以8个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从A点出,以4个单位长度/秒向右运动.设数轴上的点N到原点O的距离等于P点到O的距离的一半,有两个结论①ON+AQ的值不变;②ON-AQ的值不变.请判断那个结论正确,并求出结论的值.
为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段以达到节水的目的. 该市自来水收费价格见价目表.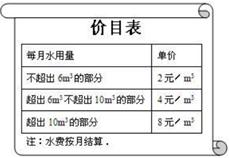
(1)填空:若该户居民2月份用水4m3,则应收水费元;
(2)若该户居民3月份用水am3(其中6<a<10),则应收水费多少元?(用a的整式表示并化简)
(3)若该户居民4,5月份共用水15m3(5月份用水量超过了4月份),设4月份用水xm3,求该户居民4,5月份共交水费多少元?(用x的整式表示并化简)
某自行车厂计划每天平均生产n辆自行车,而实际产量与计划产量相比有出入.下表记录了某周五个工作日每天实际产量情况(超过计划产量记为正、少于计划产量记为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 实际生产量 |
+5 |
-2 |
-4 |
+13 |
-3 |
(1)用含n的代数式表示本周前三天生产自行车的总数;
(2)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,当n=100时,那么该厂工人这一周的工资总额是多少元?
(3)若将上面第(2)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,则这一周工人的工资与按日计件的工资哪一个更多?请说明理由.
“囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
(1)用含有x、y的代数式表示右图中“囧”的面积;
(2)当y= ,x=4时,求此时“囧”的面积.
,x=4时,求此时“囧”的面积.
化简或化简求值(每小题6分,共12分)
(1)|a-2|+(b+3)2=0,求3a2b-[2ab2-2(ab-1.5a2b)+ab]+3ab2的值;
(2)已知有理数a、b、c在数轴上的对应点如图所示,化简:|b-a|+|a+c|-2|c-b|.