已知：如图，O为数轴的原点，A，B分别为数轴上的两点，A点对应的数为-30，B点对应的数为100.
（1）A、B间的距离是 ；
（2）若点C也是数轴上的点，C到B的距离是C到原点O的距离的3倍，求C对应的数；
（3）若当电子P从B点出发，以6个单位长度/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以4个单位长度/秒的速度向左运动，设两只电子蚂蚁在数轴上的D点相遇，那么D点对应的数是多少？
（4）若电子蚂蚁P从B点出发，以8个单位长度/秒的速度向右运动，同时另一只电子蚂蚁Q恰好从A点出，以4个单位长度/秒向右运动.设数轴上的点N到原点O的距离等于P点到O的距离的一半，有两个结论①ON+AQ的值不变；②ON-AQ的值不变.请判断那个结论正确，并求出结论的值.
如图，在⊙O中，CD为⊙O的直径，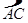
=
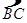，点E为OD上任意一点(不与O、D重合).求证：AE=BE.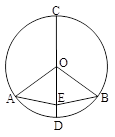
如图1、图2分别是10×6的正方形网格，网格中每个小正方形的边长均为1，线段AB的端点A、B均在小正方形的顶点上.
（1）在图1中以AB为边作锐角三角形ABC，使其为轴对称图形（点C在小正方形的顶点上）（画一个即可）;
（2）在图2中以AB为边作四边形ABDE（非正方形，点D、E均在小正方形的顶点上），使其为轴对称图形且面积为20（画一个即可）.
先化简，再求代数式
的值，其中，
.
如图1，AB∥CD，EOF是直线AB、CD间的一条折线．
（1）说明：∠O=∠BEO+∠DFO．
（2）如图2，如果将折一次改为折二次，如图2，则∠BEO、∠O、∠P、∠PFC会满足怎样的关系，证明你的结论．
（3）若将折线继续折下去，折三次，折四次折n次，又会得到怎样的结论？（不需证明）
某蔬菜公司收购到某种蔬菜280吨，准备加工后上市销售.该公司的加工能力是：每天可以精加工12吨或者粗加工32吨.现计划用15天完成加工任务，该公司应安排几天粗加工，几天精加工，才能按期完成任务？如果每吨蔬菜粗加工后的利润为1500元，精加工后为3000元，那么该公司出售这些加工后的蔬菜共可获利多少元？