为落实“两免一补”政策，腾冲县2013年投入教育经费2500万元，预计2015年投入教育经费3600万元，已知2013年到2015年的教育经费投入以相同的百分率逐年增长。
（1）求每年的平均增长率。
（2）按该平均增长率请你帮计算一下2016年腾冲县投入的教育经费为多少万元？
上个月，商店共卖出甲、乙两种商品1000件，这个月甲商品多卖出50%，乙商品少卖出10%，结果产品的总销量减少了4%，上个月甲、乙两种商品各卖出多少件？
解下列各题：
（1）解方程组
（2）化简：
（3）解不等式：
≤
，并把它的解集表示在数轴上
（4）解不等式组：
，并把它的解集表示在数轴上．
已知抛物线y=ax2+bx+3与y轴的交点为A，点A与点B关于抛物线的对称轴对称，二次函数y=ax2+bx+3的y与x的部分对应值如下表：
| x |
… |
﹣1 |
0 |
1 |
3 |
4 |
… |
| y |
… |
8 |
0 |
0 |
… |
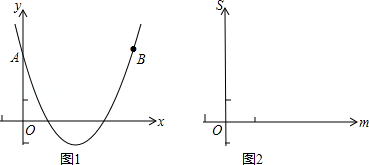
（1）抛物线的对称轴是_________ ．点A（______，____），B（_____，_____）；
（2）求二次函数y=ax2+bx+3的解析式；
（3）已知点M（m，n）在抛物线y=ax2+bx+3上，设△BAM的面积为S，求S与m的函数关系式、画出函数图象．并利用函数图象说明S是否存在最大值，为什么？
某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）与每件销售价x（元）的关系数据如下：
| x |
30 |
32 |
34 |
36 |
| y |
40 |
36 |
32 |
28 |
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式；（不写出自变量x的取值范围）
（2）如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？
如图，已知等边
，以边BC为直径的半圆与边AB,AC分别交于点D、E,过点D作DF⊥AC于点F，
（1）判断DF与⊙O的位置关系，并证明你的结论；
（2）过点F作FH⊥BC于点H，若等边的边长为8，求AF，FH的长。