如图所示,两根相距为L的金属轨道固定于水平面上,导轨电阻不计;一根质量为m、长为L、电阻为R的金属棒两端放于导轨上,导轨与金属棒间的动摩擦因数为μ,棒与导轨的接触电阻不计。导轨左端连有阻值为2R的电阻。轨道平面上有n段竖直向下的宽度为a、间距为b的匀强磁场(a>b),磁感应强度为B。金属棒初始位于OO’处,与第一段磁场相距2a。求:
(1)若金属棒有向右的初速度v0,为使金属棒保持v0的速度一直向右穿过各磁场,需对金属棒施加一个水平向右的拉力。求金属棒不在磁场中受到的拉力F1和在磁场中受到的拉力F2的大小;
(2)在(1)的情况下,求金属棒从OO’开始运动到刚离开第n段磁场过程中,拉力所做的功;
(3)若金属棒初速度为零,现对其施以水平向右的恒定拉力F,使棒刚进入各磁场时的速度都相同,求金属棒从OO’开始运动到刚离开第n段磁场整个过程中导轨左端电阻上产生的热量。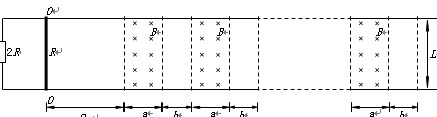
渔民为便于观察鱼塘水下的情景,设想一种方案,在水下某一深度处安装可以旋转的平面镜M,开始时平面镜是水平的,在平面镜中心O点正上方有一点光源S,发出一条光线,垂直地射到平面镜的O点上,如图所示,当平面镜绕垂直于纸面的轴O以角速度ω顺时针方向匀速转动时,在液面上观察,发现液面上有一光斑掠过,且光斑到P点后立即消失,经测量得AP=L,设水的折射率n=2,求: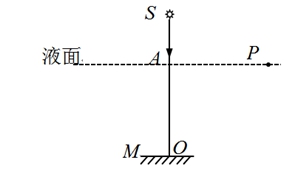
①反射光线的角速度ω′
②平面镜置于液体中的深度。
如图所示,一绝热气缸倒立竖放在两水平台面上,缸内一光滑活塞密封了一定质量的理想气体。在活塞下挂有一物块,活塞与物块的总重力G="30" N,活塞的横截面积S=3.0×l0-3m2。活塞静止时,缸内气体温度t1=27oC,体积V1=3.0×l0-3m3,外界的大气压强恒为p0= 1.0×105Pa。缸内有一个电阻丝,电阻丝的电阻值恒为R=5.0Ω,电源电动势E="18" V、内阻r="1.0" Ω。闭合开关20 s后,活塞缓慢下降高度h="0.10" m,求这20 s内气体内能的变化量和20 s末缸内气体的温度。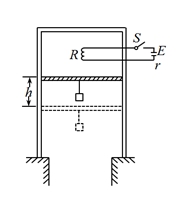
如图是检验某种平板承受冲击能力的装置,MN为半径R="0.8" m、固定于竖直平面内的光滑圆弧轨道,轨道上端切线水平,O为圆心,OP为待检验平板,M、O、P三点在同一水平线上,M的下端与轨道相切处放置竖直向上的弹簧枪,可发射速度不同但质量均为m=0.01kg的小钢珠,小钢珠每次都在M点离开弹簧枪。某次发射的小钢珠沿轨道经过N点时恰好与轨道无作用力,水平飞出后落到OP上的Q点,不计空气阻力,取g=10m/s2。求:
(1)小钢珠经过N点时速度的大小vN;
(2)小钢珠离开弹簧枪时的动能Ek;
(3)小钢珠在平板上的落点Q与圆心O点的距离s
如图所示,一水平方向的传送带以恒定的速度v=2 m/s沿顺时针方向匀速转动,传送带右端固定着一光滑的四分之一圆弧面轨道,并与弧面下端相切.一质量为m=1 kg的物体自圆弧面轨道的最高点由静止滑下,圆弧面轨道的半径R=0.45 m,物体与传送带之间的动摩擦因数为μ=0.2,不计物体滑过曲面与传送带交接处时的能量损失,传送带足够长,g=10 m/s2.求: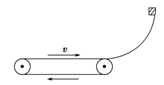
(1)物体第一次从滑上传送带到离开传送带所经历的时间;
(2)物体第一次从滑上传送带到离开传送带的过程中,传送带对物体做的功及由于摩擦产生的热量.
如图所示在水平地面上固定一个半径为R的半圆形轨道,其中圆弧部分光滑,水平段长为L,一质量为m的小物块紧靠一根被压缩的弹簧固定在水平轨道的最右端,小物块与水平轨道间的动摩擦因数为μ,现突然释放小物块,小物块被弹出,恰好能够到达圆弧轨道的最高点A,弹簧长度忽略不计,求: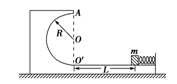
(1)小物块的落点距O′的距离;
(2)小物块释放前弹簧具有的弹性势能.