如图,已知
的两条角平分线
和
相交于
,
,
在
上,且
. 
(Ⅰ)证明:
、
、
、
四点共圆;
(Ⅱ)证明:
平分
.
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(1)求圆O和直线 的直角坐标方程;
的直角坐标方程;
(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
对于任意实数
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
已知函数
(1)若函数 在定义域内单调递增,求
在定义域内单调递增,求 的取值范围;
的取值范围;
(2)若 且关于x的方程
且关于x的方程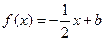 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)设各项为正的数列 满足:
满足: 求证:
求证:
如图,⊙ 的直径
的直径 的延长线与弦
的延长线与弦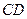 的延长线相交于点
的延长线相交于点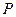 ,
,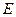 为⊙
为⊙ 上一点,AE=AC ,
上一点,AE=AC ,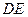 交
交 于点
于点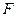 ,且
,且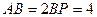 ,
,
(1)求 的长度.
的长度.
(2)若圆F且与圆 内切,直线PT与圆F切于点T,求线段PT的长度
内切,直线PT与圆F切于点T,求线段PT的长度