设某市现有从事第二产业人员100万人,平均每人每年创造产值a万元(a为正常数),现在决定从中分流x万人去加强第三产业。分流后,继续从事第二产业的人员平均每人每年创造产值可增加2x%(0<x<100)。而分流出的从事第三产业的人员,平均每人每年可创造产值1.2a万元。
(1)若要保证第二产业的产值不减少,求x的取值范围;
(2)在(1)的条件下,问应分流出多少人,才能使该市第二、三产业的总产值增加最多?
已知⊙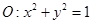 和点
和点 .
.
(Ⅰ)过点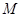 向⊙
向⊙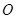 引切线
引切线 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)求以点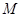 为圆心,且被直线
为圆心,且被直线 截得的弦长为4的⊙
截得的弦长为4的⊙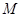 的方程;
的方程;
(Ⅲ)设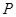 为(Ⅱ)中⊙
为(Ⅱ)中⊙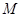 上任一点,过点
上任一点,过点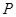 向⊙
向⊙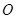 引切线,切点为
引切线,切点为 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点 ,使得
,使得 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
已知数列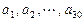 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;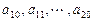 是公差为
是公差为 的等差数列;
的等差数列;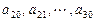 是公差为
是公差为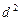 的等差数列(
的等差数列(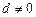 ).
).
(1)若 ,求
,求 ;
;
(2)试写出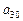 关于
关于 的关系式,并求
的关系式,并求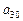 的取值范围;
的取值范围;
(3)续写已知数列,使得 是公差为
是公差为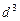 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
已知函数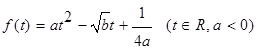 的最大值为正实数,集合
的最大值为正实数,集合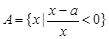 ,集合
,集合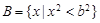 。
。
(1)求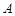 和
和 ;
;
(2)定义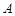 与
与 的差集:
的差集: 且
且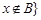 。
。
设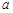 ,
, ,
,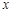 均为整数,且
均为整数,且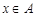 。
。 为
为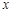 取自
取自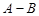 的概率,
的概率,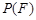 为
为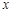 取自
取自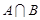 的概率,写出
的概率,写出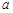 与
与 的二组值,使
的二组值,使 ,
, 。
。
(3)若函数 中,
中, ,
, 是(2)中
是(2)中 较大的一组,试写出
较大的一组,试写出 在区间[
在区间[ ,n]上的最大值函数
,n]上的最大值函数 的表达式。
的表达式。
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数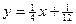 图象上的点,点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)顺次为x轴正半轴上的点,其中x1=a(0<a<1),对于任意n∈N,点An、Bn、An+1构成以
图象上的点,点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)顺次为x轴正半轴上的点,其中x1=a(0<a<1),对于任意n∈N,点An、Bn、An+1构成以
Bn为顶点的等腰三角形。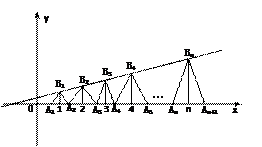
⑴求{yn}的通项公式,且证明{yn}是等差数列;
⑵试判断xn+2-xn是否为同一常数(不必证明),并求出数列{xn}的通项公式;
⑶在上述等腰三角形AnBnAn+1中,是否存在直角三角形?若有,求出此时a值;
若不存在, 请说明理由。
已知 之间满足
之间满足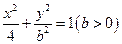
(1)方程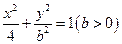 表示的曲线经过一点
表示的曲线经过一点 ,求b的值
,求b的值
(2)动点(x,y)在曲线 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;
(3)由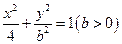 能否确定一个函数关系式
能否确定一个函数关系式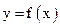 ,如能,求解析式;如不能,再加什么条件就可使
,如能,求解析式;如不能,再加什么条件就可使 之间建立函数关系,并求出解析式。
之间建立函数关系,并求出解析式。