设 ,且
,且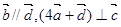 .
.
(1)求 和
和 ; (2)求
; (2)求 在
在 方向上的投影; (3)求
方向上的投影; (3)求 和
和 ,使
,使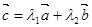 .
.
某工厂生产 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
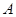 |
7 |
7 |
7.5 |
9 |
9.5 |
 |
6 |
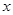 |
8.5 |
8.5 |
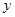 |
由于表格被污损,数据 看不清,统计员只记得
看不清,统计员只记得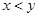 ,且
,且 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(Ⅰ)求表格中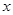 与
与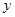 的值;
的值;
(Ⅱ)若从被检测的5件 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率.
设复数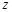 满足
满足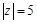 ,且
,且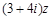 在复平面上对应的点在第二、四象限的角平分线上,
在复平面上对应的点在第二、四象限的角平分线上, ,求
,求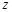 和
和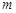 的值.
的值.
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
| 偏重 |
不偏重 |
合计 |
|
| 偏高 |
|||
| 不偏高 |
|||
| 合计 |
(2)请问该校17至18周岁的男生身高与体重是否有关?
已知函数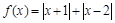 ,不等式
,不等式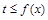 在
在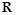 上恒成立.
上恒成立.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)记 的最大值为
的最大值为 ,若正实数
,若正实数 满足
满足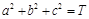 ,求
,求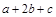 的最大值.
的最大值.
在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知曲线 的参数方程为
的参数方程为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)将曲线 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)判断曲线 与曲线
与曲线 的交点个数,并说明理由.
的交点个数,并说明理由.