如图,抛物线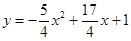 与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)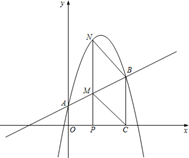
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点产作PN⊥x轴,交直线AB于点M,交抛物线于点N,设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并求出线段MN的最大值;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
仔细阅读下面解方程组得方法,然后解决有关问题:
解方程组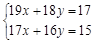 时,如果直接消元,那将时很繁琐的,若采用下面的解法,则会简单很多。
时,如果直接消元,那将时很繁琐的,若采用下面的解法,则会简单很多。
(1)请你采用上述方法解方程组: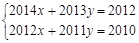
(2)请你采用上述方法解关于x,y的方程组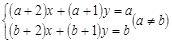 .
.
李老师想为她所任教的初二(2)班的同学购买学习用品,了解到商店每个书包的价格比每本词典多8元,用124元恰好可以买到3个书包与2本词典。
(1)每个书包和每本词典的价格分别是多少元;
(2)李老师计划用1000元为全班40位学生每人购买一件学习用品(一个书包或一本词典)后,余下不少于100元且不超过120元的钱购买体育用品,共有哪几种购买书包和词典的方案?
在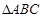 中,
中,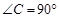 ,
,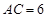 ,
,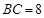 ,将
,将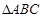 沿某条直线折叠,使三角形的顶点A与B重合,折痕为DE.
沿某条直线折叠,使三角形的顶点A与B重合,折痕为DE.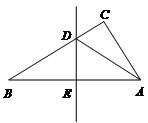
(1)试求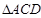 的周长;
的周长;
(2)若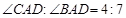 ,求
,求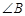 的度数。
的度数。
在一个正多边形中,一个外角的度数等于一个内角度数的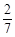 ,求这个正多边形的边数和它一个内角的度数。
,求这个正多边形的边数和它一个内角的度数。
按下列要求正确画出图形:
(1)已知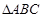 和直线PQ,画出
和直线PQ,画出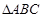 关于直线PQ对称的
关于直线PQ对称的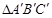 ;
;
(2)已知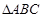 和点O,画出
和点O,画出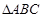 关于点O成中心对称的
关于点O成中心对称的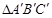 .
.